こんにちは、毛利です。
最近はChatGPTやLLMが盛り上がっていますね。趣味の一つに自作プログラミング言語・コンパイラがあるのですが、LLMと組み合わせてなんかできないかなぁと妄想しています。この記事ではcandleというライブラリを使って自作言語の言語モデルを自作(学習)してみた話について書きます。
TL;DR
- candleというHuggingFaceが作っているRust言語で書けるライブラリについて一通り書いています
- 学習させるのは自然言語ではなく、LLM向きに設計した言語を学習させることにしました。手始めに、数字の順番を逆に記述した2進数の加算の式を言語としてみました。例えば、111 + 1 = 0001. のようなものです
- candleを使った言語モデルの実装を行いました。実装はすべて記事中に記載しています
- 結果として、今回の実験の設定では数字の順番を逆にすると少ない学習量でも精度がでる言語モデルが作れることがわかりました
Rustについて
初めにcandleが使っているRust言語の話をします。
公式サイトによれば、Rust言語はパフォーマンス、信頼性、生産性に重きを置いているようです。
パフォーマンスに関しては、エネルギー効率がかなり高い(実質パフォーマンス)、といった話であったり、GitHubのコード検索にRustが使われ始めたり、GCがないメリットからdiscordで使われていたり、といった話があります。実際書いていてもC++と同じぐらいか早いぐらいの速度がでる印象です。
信頼性に関しては、所有権という仕組みによって、GCなしでもメモリ管理が適切に行われつつ、怪しい操作はコンパイル時に落としてくれるようになっています。最近感じているメリットは、並列で走るタイプのコードを書いているときに、スレッドセーフなものを使う/使わないを気にしなくていいことです。だめなときはコンパイル時に落としてくれるので、実はスレッドセーフな構造体を使わないといけなかった、みたいなところに脳を割かなくていいのがうれしいです。
生産性に関しては、rustupによるRustのバージョン管理や、cargoによる依存関係管理・ビルドが非常に楽です。フォーマッタ(cargo fmt)やlinter(clippy)も公式で存在します。また、Rust界隈は公式ドキュメントがとても丁寧なことが多く、基本的に公式ドキュメント(docs.rs)とリポジトリのexamplesを見に行くと大抵の調べたいことがわかります。
自分はRustを書き始めた5年前ぐらいから、趣味のプログラミングはほぼすべてRustで書いています。派閥がありそうなところでいうと、フロントエンドはyew(+trunk), バックエンドはactix-webを使うことが多いです。さてRustばかり書いていた結果、大抵の場合Pythonが使われる機械学習系の実装はほぼほぼノータッチになっていたのですが、最近のLLMブームで気になっていたところ、Rustで書けるcandleというライブラリが出ていたのでついに手を出してみました。
candleについて
さて、Rustで書けるcandleという機械学習ライブラリが出ていました。これについて書きます。candleのリポジトリのURLは https://github.com/huggingface/candle です。
URLからわかる通り、candleを作っているのはなんとHuggingFaceです。HuggingFaceがここにリソースを割くってのが自分は少しびっくりしましたが、Pythonのつらいポイントは業務でめちゃくちゃ感じてるので、そういうモチベーションがあっても不思議ではないかぁとも思います。
他の機械学習フレームワークに対してcandleはどういったところが良いのか?といったところですが、これはREADMEに書いてあります。
https://github.com/huggingface/candle#why-should-i-use-candle
適当に訳すと、
1. サーバーレスな推論ができるように。PyTorchのようなフレームワークはでかすぎるのでバイナリを軽くしたい
2. 運用ワークロードからPythonを取り除きたい。特にパフォーマンスやGIL(Global Interpriter Lock)の観点から
3. Rustは素晴らしい〜〜〜 ちなみにHuggingFaceのエコシステムの多くはRustのcrate(ライブラリ)がすでにある
といったところでしょうか。coolの訳難しいですね...
1. は最近悩んでいる部分を考えるとたしかになぁと思うところがあって、例えば、HuggingFaceの各モデルのページにあるHosted inference APIのComputeボタンがありますが、こういったものをシステムとして提供しようとすると、Imageはでかい、リソースの要求量はでかい、GPUもほしい、でほぼほぼKubernetesの常時起動一択みたいになってちょっとつらい、というのはありますよね(遠い目)。
2. は...まぁこれもちょっとわかりますね。
Global Interpriter Lockは最近業務でPythonを書いていて知りました。出会ったのは並列(特にマルチスレッド)化しようとしたときで、CPUバウンドな処理のマルチスレッドが性能でない、とのことでつらくなりました。まぁ抽象機械使うタイプの言語を実装してねといわれたらとりあえずそうする気はするので、そういうもんかなぁという気もします。一応Python側でGIL解消に向けての動きはあるようですね。 PEP 703 – Making the Global Interpreter Lock Optional in CPython | peps.python.org
ここで型が挙げられてないのは少し不思議ですが、Tensor型が実質Objectみたいな使い方になるので機械学習本体としては型はあんまりメリットにならない、より正確にはメリットになる型の使い方をできていない、といったところでしょうか。
3. はまぁそうですね、少なくとも趣味レベルでは論理に先行してRustを使いたいです。。
ちなみにcandleは普通にGPU(正確にはNVIDIA GPU)が使えます。後に書くコードでもGPUを使った学習を行いました。
何を学習させるか?
さて、何かを学習させるコードを書くわけですが、最近激アツの言語モデルを作りたいと思います。
言語モデルということでなんらかの言語を学習させるわけですが、趣味レベルでは自然言語にそんなに興味はなく、「言語モデル向きの言語を作り、個人でも学習できるサイズの言語モデルを学習し、それをしゃべらせて何らかのシステムを構築する」ことに興味があります。特に、思考に関する部分について、LLMが使う言語は自然言語でなくていいと思っており、例えば、Chain of Thought なり ReAct なりを人工言語で動かすといった感じです。
というわけで手始めに二進数の足し算ができる言語モデルを作ることにしました。
さて、ここで一つ試したいと思っていたことを試したいと思います。
自作プログラミング言語を考えていたときにどうしようか迷った、というか今も迷ってる仕様があり、それは数を書くときの数字の順番を逆にするというものです。例えば、123は321と書く、といった感じですね。
メリットとしては、足し算などをするときに、記述順に計算していけるというのがあります。
例えば、456 + 789は6+9から計算しますが、これは普通の日本語の順だと後ろの方から計算していく形になります。一方、逆順に書いた場合は、654 + 987 = 5421となり、前から順に繰り上がりの計算ができます。
これはGPT系統の言語モデル向きでもあると思っていて、前から書かないといけない言語モデルにおいて、加・減?・乗算を計算順に出力できる点が向いているのではと思っています。普通の順番の場合、繰り上がりをエスパーして先に上位の桁から出力するみたいな芸当が要求されるわけで、そりゃ精度でないでしょうと思っています。
逆順にするのは慣れてないので違和感はありますが、例えばアラビア語だと普通の文が右から左に書くのに対して数字の順番は下の位から(つまり日本語と見た目は同じ順)みたいなので、ありだとは思うんですよね。慣れれれば。...慣れれればがネックで、自作プログラミング言語に入れるか迷っている最大の理由ではあります。流暢に認識できるかというとたぶん大変だよなぁと。
まぁいろいろ思うところはありますが、一回やってみたかったので、数字順反転の式を学習させてみました。
candleの基本構造体
Tensor
docs: Tensor in candle_core - Rust (docs.rs)
基本的にcandleを使った計算はほぼほぼTensor型になります。
「機械学習でよく使う操作が使える多次元配列であり、(backprop用に)どう計算されたかの情報も持っている」、ぐらいの認識でいいと思います。
Device
docs: Device in candle_core - Rust (docs.rs)
機械学習ではCPUだけでなくGPUを使うことが多いです。基本的にはCPU/GPUでメモリ空間が別れているので、各Tensor型の値に関して、どこでデータを持つか?という部分を指定する必要があります。これに使われるのが`Device`です。
基本的には、`Device::cuda_if_available` を使っておけば十分だと思います。この関数は、CUDAが使えるならGPUになり、使えない場合はCPUのメモリを使ってくれます。
VarMap, VarBuilder
docs: VarMap in candle_nn::var_map - Rust (docs.rs), VarBuilder in candle_nn::var_builder - Rust (docs.rs)
多層のニューラルネットワークにおいて、例えば層ごとになど、パラメータの塊が複数存在することになります。それらをまとめて管理する仕組みが`VarMap`, `VarBuilder`です。パラメータのファイル保存・読み込みに関してもVarMapを使うことで実現できます。基本的には以下のようにテンプレ的に使えば十分だと思います。
let var_map = VarMap::new();
let var_builder = VarBuilder::from_varmap(&var_map, DType::F32, &device);`VarMap`,`VarBuilder`は階層化されており、例えば、`layer1/weight`, `layer1/bias`のようにパスのようなKeyに対してパラメータの塊を持ちます。`VarBulider`に`pp`という関数があり、`var_builder.pp("layer1")`は、`layer1/`下にパラメータを入れていける`VarBuilder`となります。
実装
注: この節は長いので実装にあまり興味がない場合は実行結果まで飛ぶことをおすすめします
GPT的なDecoderの構成で作りました。Masked Multi-Head Attention + Feed Forwardの多層構成でPre-Normです。
Transformerについては下記記事・動画がわかりやすかったです。
- How does GPT-3 spend its 175B parameters? — LessWrong
- とりあえずパラメータ群の使われ方を知るのに
- 【深層学習】Transformer - Multi-Head Attentionを理解してやろうじゃないの【ディープラーニングの世界vol.28】#106 #VRアカデミア #DeepLearning - YouTube
元論文は下記です
- [1706.03762] Attention Is All You Need (arxiv.org)
- [2002.04745] On Layer Normalization in the Transformer Architecture (arxiv.org)
実装にはcandleのexamplesのBERTの実装を参考にしました。
実装は全体で400行ぐらいとなりました。推論をさぼってますが学習だけなら基本的なAttentionはそんなに実装量多くないですね。
一点注意点があり、PyTorch-likeに作られているのですが、自分がPyTorchに詳しくない、というか一般的な機械学習系のライブラリの使い方をろくに知らないので、いろいろ調べながら書いています。もしかしたらいたるところもうちょっといい書き方があるかもしれません。
Cargo.toml(依存関係)
Cargo.tomlのdependencyです。`candle-core`に`Tensor`や`Device`などがあり、ニューラルネットを組むのに便利な構造体等は`candle-nn`にあります。
[dependencies]
# 0.2.0 -> 0.2.1で破壊的変更入ったので一応=をつけている
candle-core = { version = "=0.2.1" }
candle-nn = { version = "=0.2.1" }
rand = { version = "0.8.5", features = ["std_rng"] }use
まずは使う構造体なり関数群のuseです。
use candle_core::{DType, Device, Module, Tensor};
use candle_nn::{
activation::Activation, embedding, layer_norm, linear, loss::cross_entropy, ops::softmax,
AdamW, Embedding, LayerNorm, LayerNormConfig, Linear, ParamsAdamW, VarBuilder, VarMap, Optimizer,
};
use rand::{thread_rng, Rng};Vocabulary
今回は7種類のTOKENとします。`_`が`<PAD>`相当、ほかはそのままです。
const VOCABS: [char; 7] = ['_', ' ', '0', '1', '+', '=', '.'];ハイパーパラメータ
次はハイパーパラメータ用の構造体を作ります。
#[derive(Debug, Clone, Copy)]
pub struct HyperParams {
// 各ベクトルの次元数
d_model: usize,
// Q,K,V行列を掛けたあとのベクトルの次元数
d_head: usize,
// Multi-Head Attentionのhead数
n_head: usize,
// トークン数
n_ctx: usize,
// TOKENの種類数
n_vocab: usize,
// Attention + Feed-Forwardの層の数
n_layer: usize,
// バッチサイズ
n_batch: usize,
}Positional Encoding
次はPositional Encodingの実装です。普通のAttention層自体には位置情報の要素がないので、先に位置情報を表すベクトルを入力に足しておく、というものですね。それぞれのトークン位置に対して、d_model次元のベクトルを作成します。
計算したそれぞれの値を使って`Tensor`型にするには、`Vec<T>`型に一列に入れておいて`Tensor::from_vec`を使うと作れます。
計算式はよく使われている三角関数の式を使いました。
fn positional_encoding_tensor(
device: &Device,
d_model: usize,
n_ctx: usize,
n_batch: usize,
) -> Tensor {
let mut pe = vec![0.0f32; d_model * n_ctx];
for pos in 0..n_ctx {
for i in 0..d_model / 2 {
pe[pos * d_model + 2 * i] =
(pos as f32 / 10000f32.powf(2.0 * i as f32 / d_model as f32)).sin();
pe[pos * d_model + 2 * i + 1] =
(pos as f32 / 10000f32.powf(2.0 * i as f32 / d_model as f32)).cos();
}
}
let pe = Tensor::from_vec(pe, (1, n_ctx, d_model), device)
.unwrap()
.repeat((n_batch, 1))
.unwrap();
pe
}Multi-Head Attention
次はMulti-Head Attentionです。まず構造体を作っておきます。
maskは後ろのトークン(ベクトル)を見れなくするための行列、qs,ks,vsはQuery,Key,Valueを作る層をHeadの数分、oはそれぞれのヘッドについてQuery,Key,Valueを使った計算をしたあとに、d_model次元のベクトルに戻す部分です。
#[derive(Debug)]
pub struct MultiHeadAttention {
mask_batch: Tensor,
// qs, ks, vs: Q,K,V行列をHeadの数だけ準備
qs: Vec<Linear>,
ks: Vec<Linear>,
vs: Vec<Linear>,
o: Linear,
params: HyperParams,
}次は初期化のコードになります。
線形層のLinearは`candle_nn::linear`を使って作れます。
impl MultiHeadAttention {
pub fn new(params: HyperParams, var_builder: VarBuilder) -> Self {
let HyperParams {
d_model,
d_head,
n_head,
n_ctx,
n_batch,
..
} = params;
// softmaxしたときに0に近くなればいいので、大きい数字を引く形でmaskを実現する
// 0を掛けるのではなくsoftmaxを見込んで加算で実現するのは、計算が軽いとかのモチベーションのはず
let mut mask = vec![0.0f32; n_ctx * n_ctx];
for i in 0..n_ctx {
for j in 0..n_ctx {
if i < j {
mask[i * n_ctx + j] = -1e9;
}
}
}
let mask = Tensor::from_vec(mask, (n_ctx, n_ctx), var_builder.device()).unwrap();
let mask_batch = mask
.reshape((1, n_ctx, n_ctx))
.unwrap()
.repeat((n_batch, 1))
.unwrap();
let mut qs = vec![];
let mut ks = vec![];
let mut vs = vec![];
for i in 0..n_head {
let q = linear(d_model, d_head, var_builder.pp(format!("att_q_{:02}", i))).unwrap();
let k = linear(d_model, d_head, var_builder.pp(format!("att_k_{:02}", i))).unwrap();
let v = linear(d_model, d_head, var_builder.pp(format!("att_v_{:02}", i))).unwrap();
qs.push(q);
ks.push(k);
vs.push(v);
}
let o = linear(n_head * d_head, d_model, var_builder.pp("att_o")).unwrap();
Self {
mask_batch,
qs,
ks,
vs,
o,
params,
}
}
}次はforward(前向きに計算する処理)の記述です。
`Tensor::reshape`は全体として同じ要素数の別の形のTensorに変える関数です。
`Tensor::transpose`は転置する関数です。0-indexedで指定した2つの番目の次元を転置します。
`Tensor::repeat`はTensorを繰り返して並べたTensorを作る関数です。
`Tensor::softmax`は指定した次元の列でsoftmaxをします。Pythonの[-1]アクセス相当の、後ろから数えて次元指定することもできます。
`Tensor::matmul`は行列積です。
...本当はこれ`Vec<Tensor>`じゃなくて一つの`Tensor`にできる気がしますが、とりあえずこれで書きました。
impl MultiHeadAttention {
fn forward(&self, xs: &Tensor) -> candle_core::Result<Tensor> {
let HyperParams {
d_model,
d_head,
n_head,
n_ctx,
n_batch,
..
} = self.params;
// ys: 各HeadについてAttentionのQKV部分を計算したTensor
let mut ys = vec![];
for i in 0..n_head {
let xs_q = self.qs[i].forward(&xs).unwrap();
let xs_k = self.ks[i].forward(&xs).unwrap();
let xs_v = self.vs[i].forward(&xs).unwrap();
// transposeは0-indexedで転置する。この場合は1, 2軸を転置で、各batchについて行列を転置できる
let xs_1 = xs_q.matmul(&xs_k.transpose(1, 2).unwrap()).unwrap();
let xs_2 = (&xs_1 / (d_head as f64).sqrt()).unwrap();
let xs_3 = (&xs_2 + &self.mask_batch).unwrap();
// candle_core::D::Minus1はpythonの配列の-1と同じ、つまり最後の軸を指す
// 最後の軸についてsoftmaxする
let xs_4 = softmax(&xs_3, candle_core::D::Minus1).unwrap();
// [n_batch, n_ctx, d_head]
let xs_5 = xs_4.matmul(&xs_v).unwrap();
ys.push(xs_5);
}
// 各Headのベクトルを連結する
// [n_batch, n_ctx, n_head * d_head]
let xs_6 = Tensor::cat(&ys, 2).unwrap();
// [n_batch * n_ctx, n_head * d_head]
let xs_6_re = xs_6.reshape((n_batch * n_ctx, n_head * d_head)).unwrap();
// [n_batch * n_ctx, d_model]
let xs_o = self.o.forward(&xs_6_re).unwrap();
// [n_batch, n_ctx, d_model]
let xs_o_re = xs_o.reshape((n_batch, n_ctx, d_model)).unwrap();
Ok(xs_o_re)
}
}Layer
MultiHeadAttention層は書けたので、これを使ってTransformerの一層分を作っていきます。
同じく構造体をまず準備します。
`LayerNorm`はLayer Normalizationを行う層で、candle側で準備されているものがあるのでそれを使います。これは`layer_norm`関数で作れます。
`dence_1`, `dence_2`はFeed Forward層用の層です。Reluのような活性化関数は`Activation`型を使うと実現できます。
#[derive(Debug)]
pub struct Layer {
layer_norm_1: LayerNorm,
attention: MultiHeadAttention,
layer_norm_2: LayerNorm,
dence_1: Linear,
dence_relu: Activation,
dence_2: Linear,
}次に初期化の処理を記述します。
impl Layer {
pub fn new(hyper_params: HyperParams, var_builder: VarBuilder) -> Self {
let HyperParams { d_model, .. } = hyper_params;
let layer_norm_1 = layer_norm(
d_model,
LayerNormConfig::default(),
var_builder.pp("layer_norm_attention"),
)
.unwrap();
let attention = MultiHeadAttention::new(hyper_params, var_builder.pp("attention"));
let layer_norm_2 = layer_norm(
d_model,
LayerNormConfig::default(),
var_builder.pp("layer_norm_dence"),
)
.unwrap();
let dence_1 = linear(d_model, 4 * d_model, var_builder.pp("dence_1")).unwrap();
let dence_relu = Activation::Relu;
let dence_2 = linear(4 * d_model, d_model, var_builder.pp("dence_2")).unwrap();
Self {
layer_norm_1,
attention,
layer_norm_2,
dence_1,
dence_relu,
dence_2,
}
}
}次にforwardの処理を記述します。こっちは一直線でシンプルですね。
impl Layer {
fn forward(&self, xs: &Tensor) -> candle_core::Result<Tensor> {
// attention
let xs_1 = self.layer_norm_1.forward(&xs).unwrap();
let xs_2 = self.attention.forward(&xs_1).unwrap();
let xs_3 = (&xs_2 + xs).unwrap();
// feed-forward
let xs_4 = self.layer_norm_2.forward(&xs_3).unwrap();
let xs_5 = self.dence_1.forward(&xs_4).unwrap();
let xs_6 = self.dence_relu.forward(&xs_5).unwrap();
let xs_7 = self.dence_2.forward(&xs_6).unwrap();
let xs_8 = (&xs_7 + &xs_3).unwrap();
Ok(xs_8)
}
}言語モデル全体
最後に言語モデル全体を表す構造体を作ります。
#[derive(Debug)]
pub struct LanguageModel {
// Token ID -> d_model次元ベクトルへの変換
embedding: Embedding,
positional_encoding_tensor: Tensor,
layers: Vec<Layer>,
output_linear: Linear,
}次に初期化の実装です。
indexに対応してベクトルを持つ仕組みは`Embedding`構造体を使うと実現でき、これは`embedding`関数で作れます。
impl LanguageModel {
pub fn new(device: &Device, hyper_params: HyperParams, var_builder: &VarBuilder) -> Self {
let HyperParams {
d_model,
n_ctx,
n_vocab,
n_layer,
n_batch,
..
} = hyper_params;
let embedding = embedding(n_vocab, d_model, var_builder.pp("embedding")).unwrap();
let positional_encoding_tensor =
positional_encoding_tensor(&device, d_model, n_ctx, n_batch);
let mut layers = vec![];
for i in 0..n_layer {
let layer = Layer::new(hyper_params, var_builder.pp(format!("layer_{:02}", i)));
layers.push(layer);
}
let output_linear = linear(d_model, n_vocab, var_builder.pp("output_linear")).unwrap();
LanguageModel {
embedding,
positional_encoding_tensor,
layers,
output_linear,
}
}
}次にforwardの実装です。
impl LanguageModel {
pub fn forward(&self, xs: &Tensor) -> candle_core::Result<Tensor> {
// embedding
let xs_1 = self.embedding.forward(&xs).unwrap();
// positional encoding
let xs_2 = (&xs_1 + &self.positional_encoding_tensor).unwrap();
// layers
let mut xs_3 = xs_2.clone();
for layer in &self.layers {
xs_3 = layer.forward(&xs_3).unwrap();
}
// output
let xs_4 = self.output_linear.forward(&xs_3).unwrap();
Ok(xs_4)
}
}これでとりあえずパーツはそろいました。
学習データ作成
学習データ用の数字順反転の足し算の式を作っていきます。
まずは学習データ用構造体を作ります。それぞれのTensorの要素はVocabularyのIndexです。
#[derive(Debug)]
pub struct TrainData {
// [n_batch, n_ctx]
pub input: Tensor,
// [n_batch * n_ctx]
pub expected_output: Tensor,
}次に逆順の式を作ってそれで学習データを作る関数を作ります。
fn create_add_binary_exprs(hyper_params: HyperParams, device: &Device) -> TrainData {
let HyperParams {
n_ctx,
n_vocab,
n_batch,
..
} = hyper_params;
assert!(n_vocab == 7);
// input
let mut input = vec![0i64; n_batch * n_ctx];
let mut expected_output = vec![0i64; n_batch * n_ctx];
let mut rand = thread_rng();
let max_digits = 12;
for i in 0..n_batch {
// 桁数を1~max_digitsでuniformに持ってきて、その桁数の数をuniformに持ってきて値を作る
// 素直にuniformに持ってくると大きい桁数に偏るため
let a_digits = rand.gen_range(1..=max_digits);
let a = rand.gen_range((1 << (a_digits - 1))..(1 << a_digits));
let b_digits = rand.gen_range(1..=max_digits);
let b = rand.gen_range((1 << (b_digits - 1))..(1 << b_digits));
let c = a + b;
// 数字を書く順番を逆順ではなく普通の順番にしたいときは`.rev()`を消す
let a_s = format!("{:b}", a).chars().rev().collect::<String>();
let b_s = format!("{:b}", b).chars().rev().collect::<String>();
let c_s = format!("{:b}", c).chars().rev().collect::<String>();
let s = format!("{} + {} = {}.", a_s, b_s, c_s);
let cs = s.chars().collect::<Vec<_>>();
assert!(cs.len() < n_ctx);
for k in 0..n_ctx {
if k < cs.len() {
input[i * n_ctx + k] = VOCABS.iter().position(|&c| c == cs[k]).unwrap() as i64;
} else {
// <PAD>
input[i * n_ctx + k] = 0;
}
}
// 期待出力は入力を1ずらして作る
for k in 0..n_ctx - 1 {
expected_output[i * n_ctx + k] = input[i * n_ctx + k + 1];
}
expected_output[i * n_ctx + (n_ctx - 1)] = 0;
}
let input = Tensor::from_vec(input, (n_batch, n_ctx), device).unwrap();
let expected_output = Tensor::from_vec(expected_output, n_batch * n_ctx, device).unwrap();
TrainData {
input,
expected_output,
}
}全体作成
最後に学習データを使って計算してパラメータ更新を行うコードです。
Lossの計算には`cross_entropy`関数を使っています。
学習ですが、以下2ステップでできます
1. パラメータ調整手法のAdamを使う`AdamW`というのがあり、その値を作成
2. lossまでforwardしたら`loss.backward().unwrap()`でback propagationを計算して、`backward_step`でパラメータの更新を行う
fn main() {
let device = Device::cuda_if_available(0).unwrap();
let var_map = VarMap::new();
let var_builder = VarBuilder::from_varmap(&var_map, DType::F32, &device);
// ハイパーパラメータ一覧、Attention内外のベクトルの次元数やレイヤの数など
let hyper_params = HyperParams {
d_model: 96,
d_head: 24,
n_head: 4,
n_ctx: 64,
n_vocab: 7,
n_layer: 2,
n_batch: 192,
};
let HyperParams {
n_ctx,
n_vocab,
n_batch,
..
} = hyper_params;
// 言語モデル本体
let model = LanguageModel::new(&device, hyper_params, &var_builder);
// optimizer準備
let params = ParamsAdamW::default();
let mut optimizer = AdamW::new(var_map.all_vars(), params).unwrap();
// 学習のループ
for iter in 0..10000 {
// 学習用データ準備
let TrainData {
input,
expected_output,
} = create_add_binary_exprs(hyper_params, &device);
// forward
let output = model.forward(&input).unwrap();
// cross_entropyでloss計算
let output = output.reshape((n_batch * n_ctx, n_vocab)).unwrap();
let loss = cross_entropy(&output, &expected_output).unwrap();
let loss_f32 = loss.to_scalar::<f32>().unwrap();
eprintln!("iter = {}, loss = {}", iter, loss_f32);
// ときどき性能を表示
if iter % 100 == 99 {
eprintln!("--------------------------- iter = {}", iter);
let output_softmax = softmax(&output, candle_core::D::Minus1).unwrap();
let output_softmax_argmax = output_softmax.argmax(candle_core::D::Minus1).unwrap();
let output_softmax_argmax_vec = output_softmax_argmax.to_vec1::<u32>().unwrap();
let output_softmax_argmax_vec = output_softmax_argmax_vec
.iter()
.map(|&x| x as i64)
.collect::<Vec<_>>();
let input_vec = input
.reshape(n_batch * n_ctx)
.unwrap()
.to_vec1::<i64>()
.unwrap();
let mut count = 0;
for i in 0..n_batch {
// indexの列から文字列を復元したものと、=の後ろを切り出したものを返す関数
let f = |xs: &[i64]| {
let mut s = String::new();
for &x in xs {
let c = VOCABS[x as usize];
s.push(c);
}
let ts = s.split('=').map(|s| s.to_string()).collect::<Vec<_>>();
let ans = ts.get(1).map(|s| s.to_string()).unwrap_or("".to_string());
let ans = ans.trim_end_matches('_').to_string();
(s, ans)
};
let (s, ans_o) = f(&output_softmax_argmax_vec[i * n_ctx..(i + 1) * n_ctx]);
eprintln!("output = {}", s);
let (s, ans_i) = f(&input_vec[i * n_ctx..(i + 1) * n_ctx]);
eprintln!("input = {}", s);
eprintln!();
if ans_o == ans_i {
count += 1;
}
}
eprintln!(
"iter = {}, accuracy: {} / {}, {:.3} %",
iter,
count,
n_batch,
count as f64 / n_batch as f64 * 100.0
);
eprintln!();
}
// 学習(パラメータ更新)
loss.backward().unwrap();
optimizer.backward_step(&loss).unwrap();
}
// モデル保存
var_map.save("model.bin").unwrap();
}実行方法
実行は以下のコマンドでできます。
CUDAがない場合は--features candle-nn/cudaなしで実行してください。
cargo run --release --features candle-nn/cudafeaturesについてですが、Cargo.tomlに書いてもいいのですが、CUDAを使えない環境のCIが通らなくなるので、自分はCargo.tomlには書かない形を取りました。
実験結果
1batchあたり192文で、7000バッチぐらいでほぼ確実に正解するようになりました。実行時間としては 10000batchで RTX3060 12GB を使って30分ぐらいとなりました。
手始めにやるにはちょうどいい問題になったかなと思います。
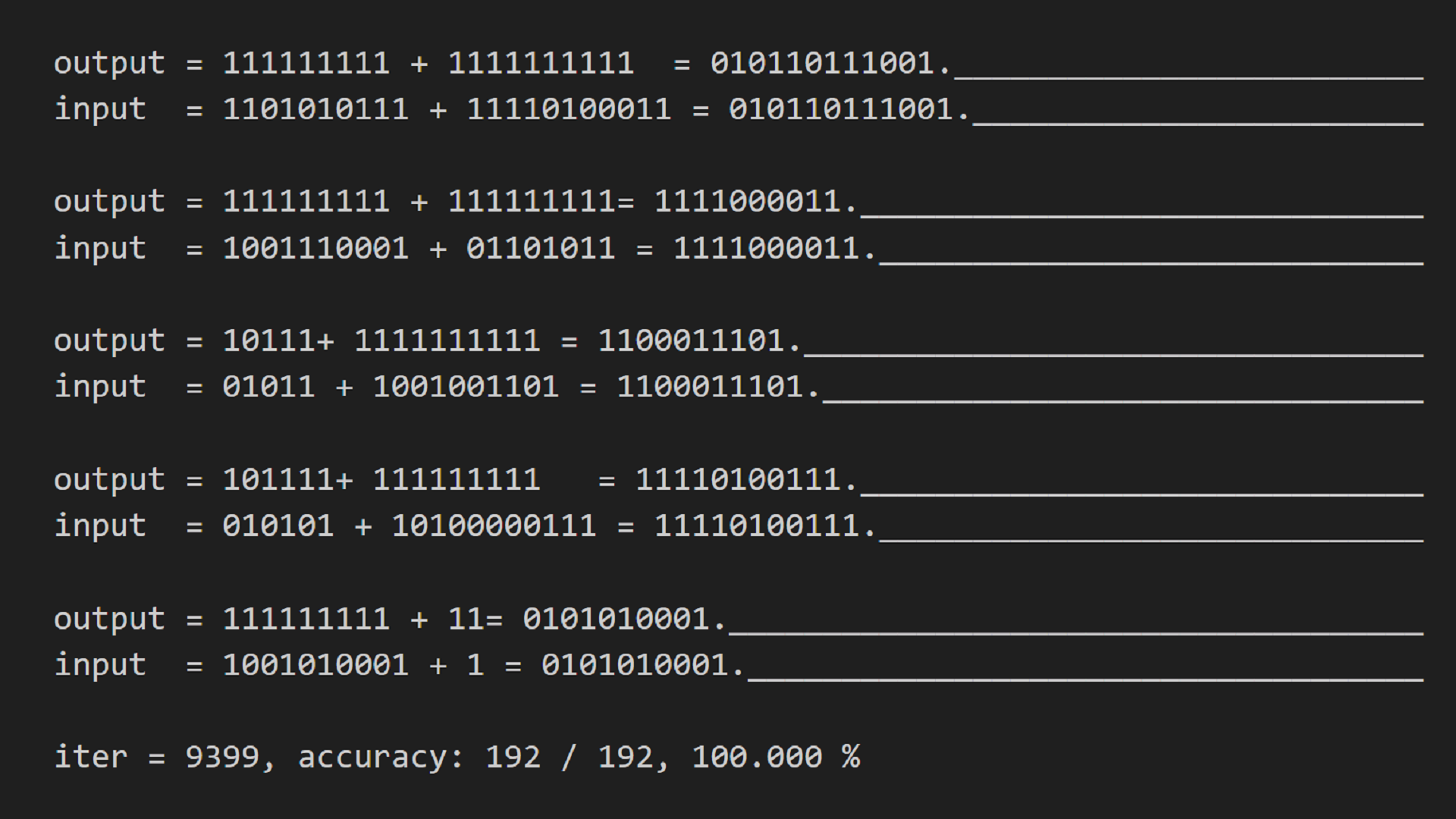
正解の様子は以下の図のようになりました。情報が揃う=以降が推測できていることがわかります。
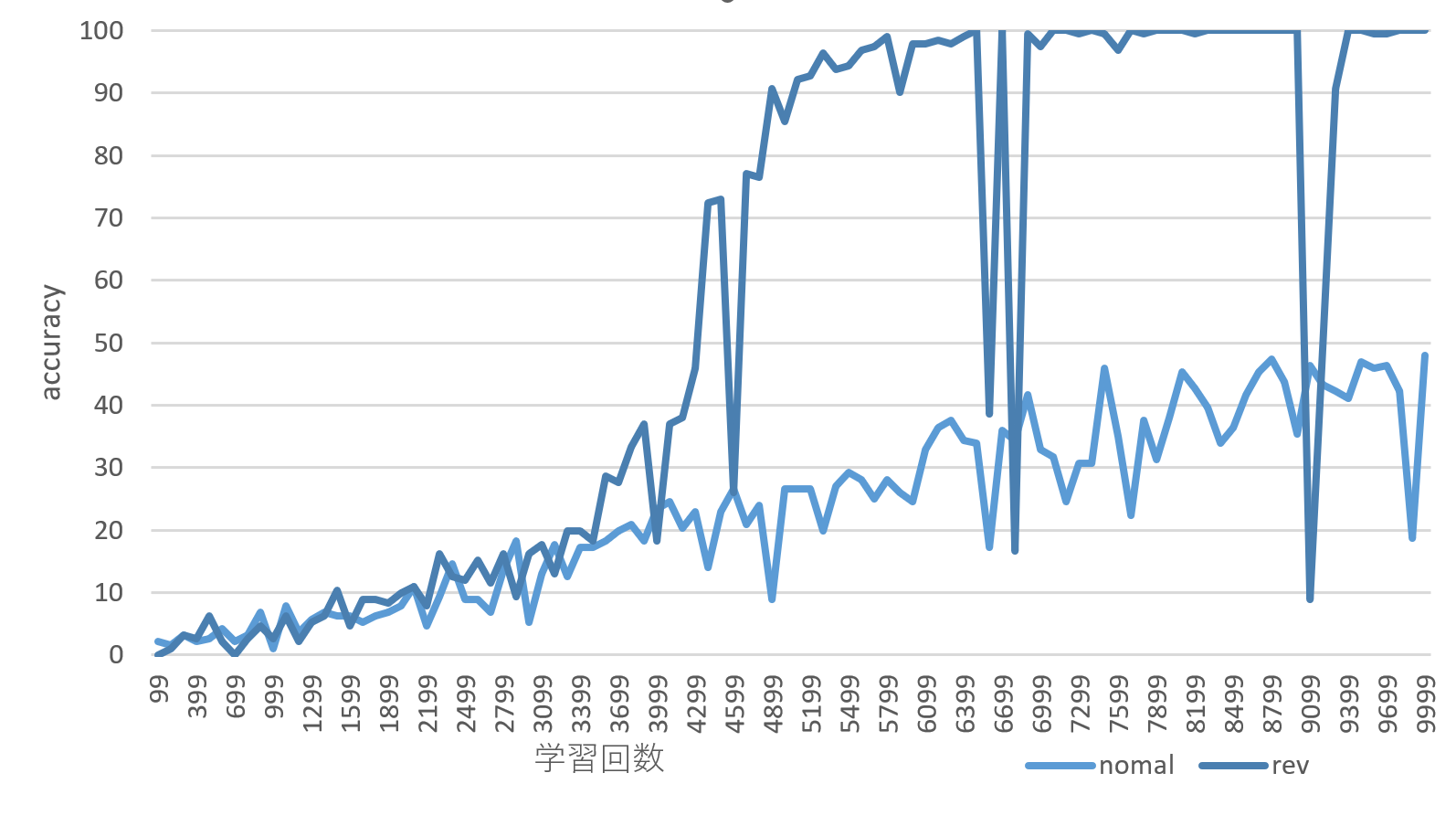
正解率の変動は以下の図のようになりました。数値の記述において、数字の順番を逆順にしたほうが正解率が上がるのが早いことがわかりました。ときどき正解率が極端に下がる場面があるのは謎です。
というわけで想像以上に良い感じに動きました。やったね。
感想
Rustで機械学習系のコードを書けるのがめちゃくちゃうれしい
うれしい。
例えば趣味で動かしてるフロント/バックRust製のStatic Web AppsのFunctionsで動くバックエンド部分にちょっとした機械学習系のコードを使うこともできそうです。わくわく。
自作言語にTensorを言語の機能としていれたいと思った
さてTensor型とかいう概念に初めてちゃんと触れましたが、結構面白かったです。
ちょっと思ったのは、これってプログラミング言語側でサポートしてもいいのでは?と思いました。実質基本型みたいなメソッドの数してますし。
ちょっと表現が難しいのですが、おそらくdefine-by-run的な部分に由来すると思うのですが、forwardとしては計算であり、backwardに使われるという意味では計算の記述でもある、みたいなコードが面白いなぁと思いました。もうちょっと言い換えるとHaskellのthunkみたいな遅延評価っぽい計算木をコード上で操作できるみたいな印象を持ちました。両方の性質を持ってるコードにあまり心当たりがないので、こういうプログラムの記述があるんだなぁというか面白いなぁと思いました。
また、素の配列よりは抽象度が低いので、最適化に使える情報量が多くなっていいんじゃないかなぁとも思いました。
追加できるといいなと思う部分としては、次元の時点で間違っている計算についてはコンパイル時に教えられるといいですね、broadcastの扱いがちょっと大変そうなのと、依存型が必要そうな気はしますが。
まぁというわけでそのうち自作言語にTensor相当を言語機能として入れようかなと思います。どのみちGPUその他もろもろを自作言語でもぶん回したいですし。...いつできあがるのかわかりませんが。
LLM向け言語の設計しがいがありそうとわかった
数字の順番を逆順に、がここまで効くと思ってなかったので、LLM向け言語の価値あるかなぁとか思っていましたが、実際やってみると結構効いてそうなので、普通に発想としてありだなぁと思いました。
次は減算ですかね、たぶん符号を後ろに持ってこればどうにか...なるか?
おわりに
Rustはいいぞ






![Microsoft Power BI [実践] 入門 ―― BI初心者でもすぐできる! リアルタイム分析・可視化の手引きとリファレンス](/assets/img/banner-power-bi.c9bd875.png)
![Microsoft Power Apps ローコード開発[実践]入門――ノンプログラマーにやさしいアプリ開発の手引きとリファレンス](/assets/img/banner-powerplatform-2.213ebee.png)
![Microsoft PowerPlatformローコード開発[活用]入門 ――現場で使える業務アプリのレシピ集](/assets/img/banner-powerplatform-1.a01c0c2.png)


