好きな教科は日本史と古典！　ガチ文系なのに中学の途中でアメリカに行ってしまったため、得意教科が０になり、理数系の道をひたすら追い求めることになってしまった（日本での）最高学歴＝小卒！　という魅惑のステータスを誇るMarketing & Salesチームの奥山です！

そんな血迷った理数系ジャングルでの迷走期、とある思想を植え付けられたのです。それは――。

コンピューターは計算ができない。

「コンピューターの計算は誤差が付き物だから、アタリをつけるのには役に立つけれど正確な答えだとは思わない方がいいよ！」

これが教授の口癖でした。

しかし数学者だって、みんながみんな、テレビや漫画のキャラクターみたいに暗算の天才というわけじゃありません。というか私は暗算できません。電卓大好き、紙と鉛筆も大好き。だからそんなこと言われても……。そもそも私は代数学が好き……。と思っていたら解析幾何学から宇宙物理の香りがしてくる理数系ジャングルの奥地にひっそり建てられたピラミッド迷宮みたいなものに迷い込んでしまったため、数字の雨が降ってくることに（NASAがある街だったからかすぐに宇宙が引っ張り出されるのが常…… ）。

もうやだっ！　算数以上のもの見たくないっ！　日常生活は有理数と計算機でアバウトに生きていけるもんっ！

と思っていたら……。

計算機が嘘をつく例としてよく挙げられる問題に出会ってしまいました（というか教授に押し売りされました）。それがこちら。

……え？　１でしょ？　小学生でも間違えないやつでしょ？

そこで取り出すのが私の相棒、CASIO SL-120！

手帳型計算機（ワイシャツの胸ポケットに入るサイズ）の可愛い子！　少なくとも35歳の電卓兄さん。

それじゃあこれに先ほどの式を打ち込んで……。

うぉい！　そうだよ、よく考えればそうなるよ！　だって$latex 1 \div 3 $は純循環小数（少数第一位からずっと同じ数字の繰り返し）だもん！

ちなみにちょっと賢い相棒は切り捨てご免もしてくれる。

が、 広がる誤差

四捨五入すれば安心する表示も出る。

でも四捨五入……。

なんてことをやっていたのが割と最近の話。７～８年くらい前でしたか。

と思いながらつい先日、暇を持て余して携帯の計算機で遊んでいたんです（何か面白い数学トリック作れないかな～）。

そこでふと思い出して打ち込んだ$latex 1 \div 3$

これに３を掛けてみると――。

あれ？　何これ、いつの間に頭良くなったの？　計算機。

いやいや騙されないぞ。きっと数字丸めてるだけでしょ？

秘儀・怒涛の0.3333333333333333333333333333333333333333333333333333333333！（階乗記号じゃありません）

よしよし、これで３を掛けてみればおのれの正体が……！

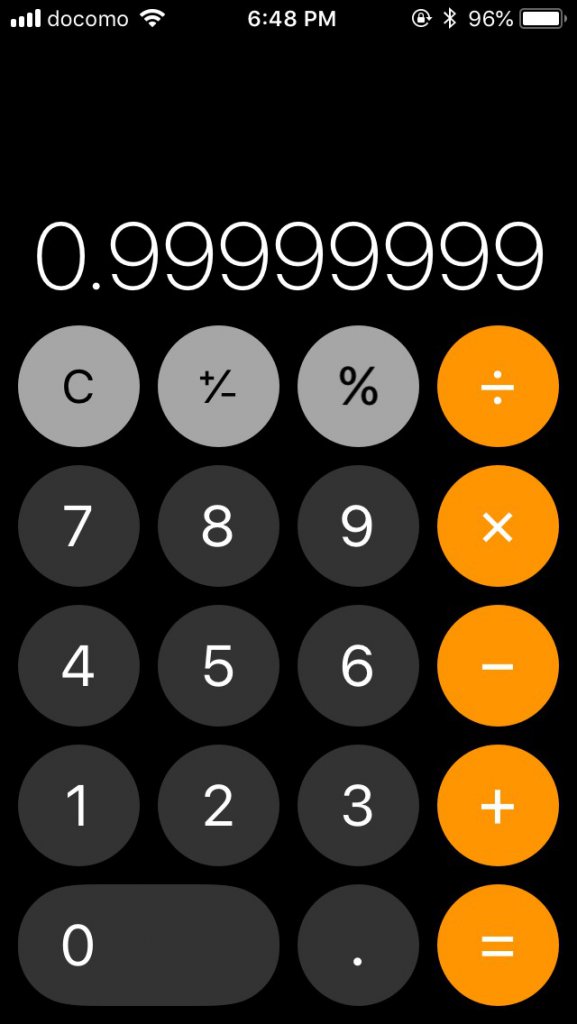
えぇぇっ⁈　貴方いつの間に計算できるようになったの⁈　（赤ん坊だった親戚がいつの間に大学生になっていた時のおばさんみたいな反応）

Androidの携帯をすぐさま取り出し計算してみましたが同じ結果。怒涛の0.3333（以下略）にも騙されません。

どうなってるの？　と思いつつGoogleさんにも同じ問題を出してみた。

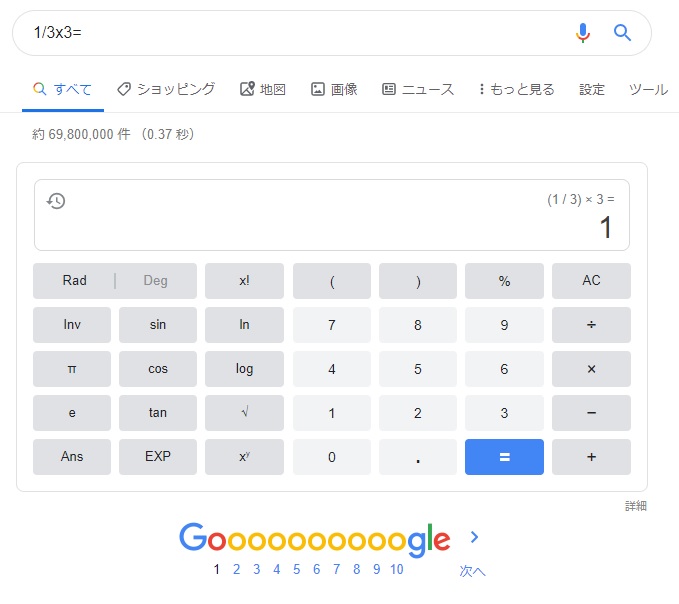
お！　まさか、そうなのね！　勝手に括弧でくくることができるようになったのね、貴方も！

感動しつつも意地悪い私はGoogleさんを騙そうと$latex 1 \div 3 $をやって一度答えを吐き出させてからの$latex \times 3 $。

しかし手強いGoogleが出した答えは１！（これは階乗ととってもいいですよ）

負けるもんかぁ！　と再び怒涛の（以下略）。しかし騙されぬ！

うーん……。駄目かもしれないけど、他の循環小数、やってみちゃう？

そうだな、できる限り一回目の計算で答えが小さくなるように$latex \frac {1}{9} &s=2$とか……？

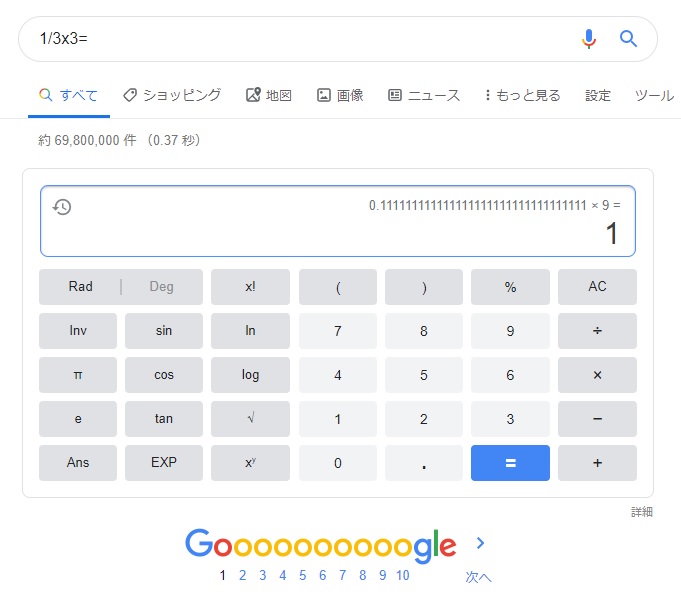
だ・ま・さ・れ・た・ゼ！

ひゃっほぅ！　ふー、いい仕事した。やれやれ、手こずらせやがって。

コンピューターでの無理数の計算はまだまだ誤差が多いようですが、有理数でもパーフェクトになりきれていないことがわかって私は今日も幸せです。コンピューターが間違えるんだから、私だって間違えていいんじゃないかという駄目な自己肯定感を得ました。

まぁ、0.9999999...=１なんでここの部分だけ見ればコンピューターも間違ってないんですけど……（でも誤差は計算を何度も重ねることで発生します）。

え？　なんでって？　その証明は下に書いておくので、暇があったら見てください。

0.9999...=1の証明は色々あるけど、一番正確な無限等比級数の公式を使うよ！

$latex 0.999... = \frac {9}{10} + \frac {9}{10} \times (\frac {1}{10})^2 + \frac {9}{10} \times (\frac {1}{10})^3 ... + \frac {9}{10} \times (\frac {1}{10})^{n-1} &s=2$

なので

初項が$latex \frac {9}{10} &s=2$で公比が$latex \frac {1}{10} &s=2$

下記の無限等比級数の公式に当てはめる。

$latex \displaystyle \sum_{n = 1}^{\infty} a_n = \frac{a_1}{1-r} &s=2$

すると

$latex \frac {\frac {9}{10}}{1-\frac{1}{10}} = 1 &s=2$

という訳で0.999... = 1になる！　やったー！