
こんにちは。FIXER M&S 竹中です。 この連載も3本目になりました。今日はKaggleのGetting Startedより住宅価格の値段を予測するコンペをやっていきましょう。前回のお題が二値分類であったのに対し、今回は連続値を予測するモデルになります。
1.今回のお題
今回はKaggleの入門データセット「House Prices: Advanced Regression Techniques 」を利用します。ボストンの住宅価格と、各住宅の諸条件を持つデータセットです。初期の特徴量が79個と多いのが特徴で、これが学習モデルの選択にも関係してきます。
2.まずはデータを見てみよう
いつも通り、ライブラリのインポートとデータの取り込みをして、訓練データの概要を見てみましょう。describeは割愛して、前回も使った欠損値抽出モジュールを使っていきます。また今回は変数が多いので欠損のあるもののみ取り出したいと思います。同時に、欠損のある変数のデータ型も取得しましょう。
import pandas as pd
import numpy as np
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import Lasso, ElasticNet
train = pd.read_csv("hp_train.csv")
test = pd.read_csv("hp_test.csv")
# サンプルから欠損値と割合、データ型を調べる関数
def Missing_table(df):
# null_val = df.isnull().sum()
null_val = df.isnull().sum()[train.isnull().sum()>0].sort_values(ascending=False)
percent = 100 * null_val/len(df)
na_col_list = df.isnull().sum()[df.isnull().sum()>0].index.tolist() # 欠損を含むカラムをリスト化
list_type = df[na_col_list].dtypes.sort_values(ascending=False) #データ型
Missing_table = pd.concat([null_val, percent, list_type], axis = 1)
missing_table_len = Missing_table.rename(
columns = {0:'欠損値', 1:'%', 2:'type'})
return missing_table_len.sort_values(by=['欠損値'], ascending=False)
Missing_table(train)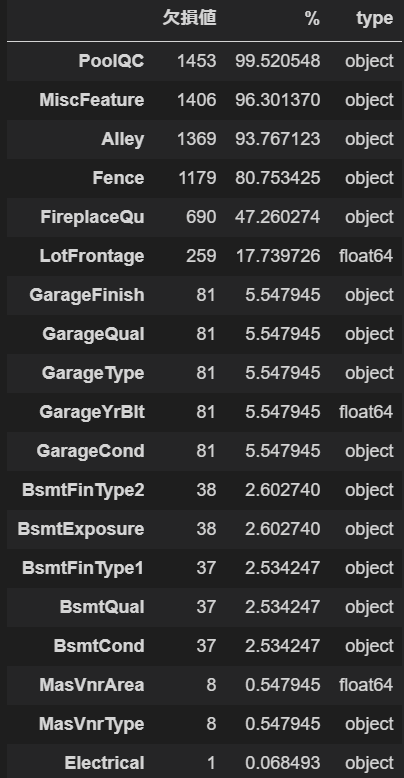
はい。こちらが欠損を含むデータの一覧です。特徴量の全量が多いので欠損も多いですね。3つが数値データであとはすべてカテゴリカルデータです。
欠損率が80%を超えているようなデータは無視してしまいたくなるのですが、ここでデータの意味を見てみましょう。今回は幸いにも"data_description.txt"というファイルがあらかじめ入っていて、各データがどういう意味を持つかを教えてくれています。それによるとPoolQCは家にあるプールの等級を示します。プール付きでない家はNA(データなし)と表示されています。また、数値データであるLotFrontageは通りから物件までの直線距離を示しています。道路に面した物件はNAとなっています。
つまり、今回のデータでは欠損は欠損でなく「値を持たない」ことが値であると言えそうです。なので、今回カテゴリカルデータはNAのまま、数値データはNAを0で埋めて学習させたいと思います。
train['WhatIsData'] = 'Train'
test['WhatIsData'] = 'Test'
test['SalePrice'] = 9999999999
alldata = pd.concat([train,test],axis=0).reset_index(drop=True)
# 訓練データ特徴量をリスト化
cat_cols = alldata.dtypes[train.dtypes=='object'].index.tolist()
num_cols = alldata.dtypes[train.dtypes!='object'].index.tolist()
other_cols = ['Id','WhatIsData']
# 余計な要素をリストから削除
cat_cols.remove('WhatIsData') #学習データ・テストデータ区別フラグ除去
num_cols.remove('Id') #Id削除
cat = pd.get_dummies(alldata[cat_cols])
# データ統合
all_data = pd.concat([alldata[other_cols],alldata[num_cols].fillna(0),cat],axis=1)
all_data.describe()
なお、データ整理の方法についてはこちらを一部参考とさせて頂きました。
欠損値を埋めた後の目的変数"SalesPrice"のヒストグラムを見てみましょう。
plt.hist(train['SalePrice'], bins=50)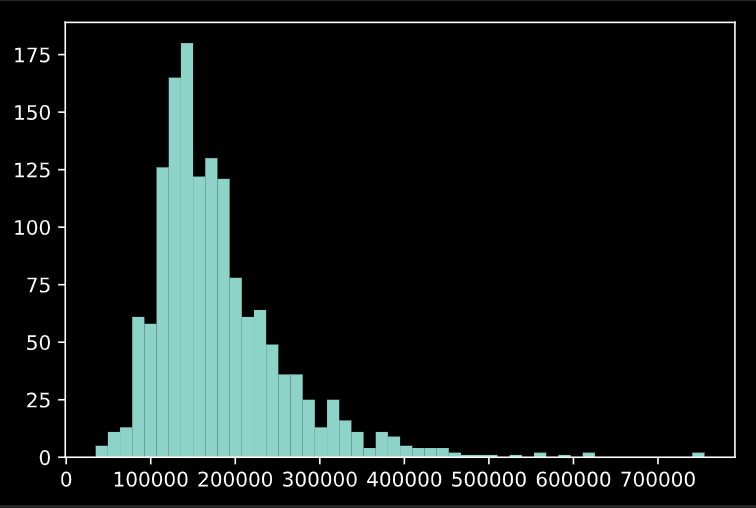
ピークは15万ドル前後でしょうか。ちょっとこのままでは使いづらいですね。ただ、こういったポアソン分布(っぽい)データは対数を取ると正規分布に近づきますので、
plt.hist(np.log(train['SalePrice']), bins=50)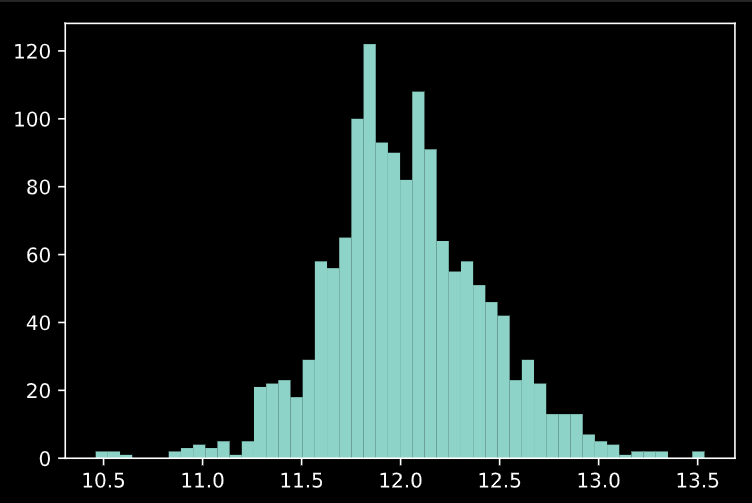
これで正規分布に近いシルエットになりました。今回は目的変数のlogを取ってモデル化したいと思います。
3.データをフィッティングしてみる
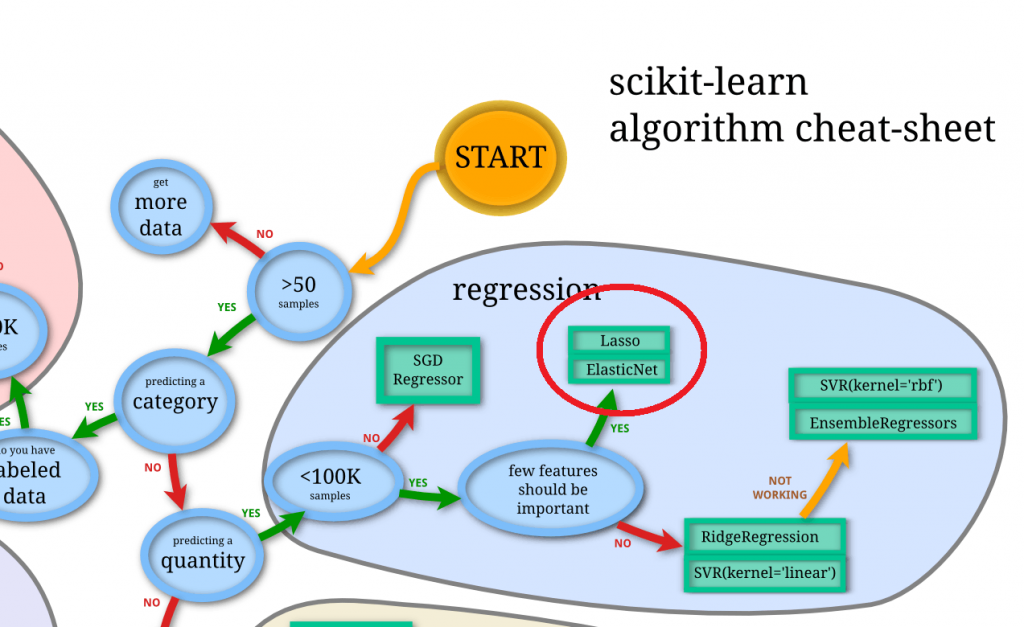
さて、前処理が終わりましたのでフィッティングにかけていきたいと思います。ざっくり選ぶべきモデルを確認したい場合、下記のSklearnのチートシートを使うのが早いです。今回は
1.数値(連続値)の予測
2.サンプルが大きすぎない
3.重要でなさそうな特徴量がある
などの特徴をみたすため、Regression(回帰)の中でもLasso回帰かElasticNetを使うのが良い、と言えそうです。 Lasso回帰もElasticNetも特徴量に強くペナルティを掛けられるため、今回のように玉石混交なデータでは有効そうです。
実際に両方にフィッティングしてみましたが、今回のデータではElasticNetの方がスコアが良さそうなので、以下ElasticNet前提で記述していきます。
また、前回と同様に精度向上のためグリッドサーチを同時に試していきましょう。調整するElasticNetのパラメータはペナルティ項のαとL1/L2ノルムの比であるl1_ratioです。
# ElasticNetによるパラメータチューニング
train_ = all_data[all_data['WhatIsData']=='Train'].drop(['WhatIsData','Id'], axis=1).reset_index(drop=True)
test_ = all_data[all_data['WhatIsData']=='Test'].drop(['WhatIsData','SalePrice'], axis=1).reset_index(drop=True)
x_ = train_.drop('SalePrice',axis=1)
y_ = train_.loc[:, ['SalePrice']]
y_ = np.log(y_)
parameters = {
'alpha' : [0.001, 0.01, 0.1, 1, 10, 100],
'l1_ratio' : [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9],
}
En = GridSearchCV(ElasticNet(), parameters)
En.fit(x_, y_)
print(f"training dataに対しての精度: {En.score(x_, y_):.2}")
test_feature = test_.drop('Id',axis=1)
prediction = np.exp(En.predict(test_feature))ちなみにトレーニングデータの目的変数のlogを取っているので、最後の行でpredictしたもののexpを取って元に戻しています。
さて、データを書き出してKaggleにアップロードしてみましょう!
# Idを取得
Id = np.array(test["Id"]).astype(int)
# my_prediction(予測データ)とPassengerIdをデータフレームへ落とし込む
result = pd.DataFrame(prediction, Id, columns = ["SalePrice"])
# my_tree_one.csvとして書き出し
result.to_csv("prediction_regression.csv", index_label = ["Id"])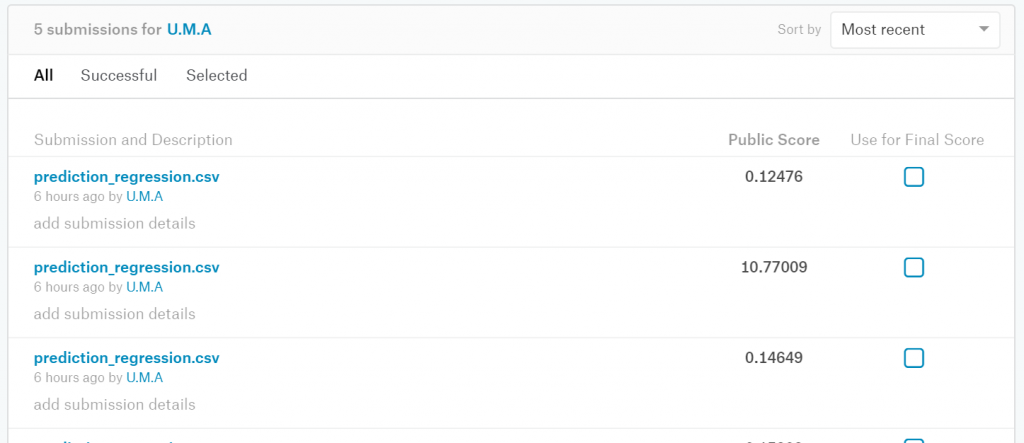
結果は真値からの平均二乗誤差(RMSE)で評価されます。私のスコアは0.12476で、ランキングは 1437位/4246位でした。前回は上位60%程度でしたので、母数は異なるとはいえ前回よりも高順位と言っていいのではないでしょうか
ちなみに、expで戻す処理を忘れてRMSEがとんでもない値になったというショボいミスもありました(笑)

以上、お読みいただきありがとうございました。
(2回連続集中線で強引にオチにしたこと、反省してます編集長)







![Microsoft Power BI [実践] 入門 ―― BI初心者でもすぐできる! リアルタイム分析・可視化の手引きとリファレンス](/assets/img/banner-power-bi.c9bd875.png)
![Microsoft Power Apps ローコード開発[実践]入門――ノンプログラマーにやさしいアプリ開発の手引きとリファレンス](/assets/img/banner-powerplatform-2.213ebee.png)
![Microsoft PowerPlatformローコード開発[活用]入門 ――現場で使える業務アプリのレシピ集](/assets/img/banner-powerplatform-1.a01c0c2.png)


