新型コロナのPCR検査を通してエンジニアが把握すべき指標を詳しく知ろう | cloud.config Tech Blog

はじめに

新型コロナウイルス感染症（COVID-19）のPCR検査や、今年1月に開始された尿一滴で行うガン検査で話題になった検査の指標について、僕たちエンジニアが機械学習モデルの利用時にも必ず考慮すべき指標だと感じたので記事にしてみようと思いました。
僕個人は数学がとても苦手で、統計には触れたことすらありません。
今回は小中学生でも計算できる検査の指標と実際の計算を通して、論理的な考察をすべきエンジニアが最低限考慮すべき指標を見ていこうと思います。

検査でよく使う指標

検査には感度と特異度という言葉がります。
一般的に感度を上げると特異度が下がる関係にあるため、その双方が高い確率である検査は優秀な検査となります。
概要を下記の表に表しましたが、それぞれの指標について詳しい説明をしていきます。

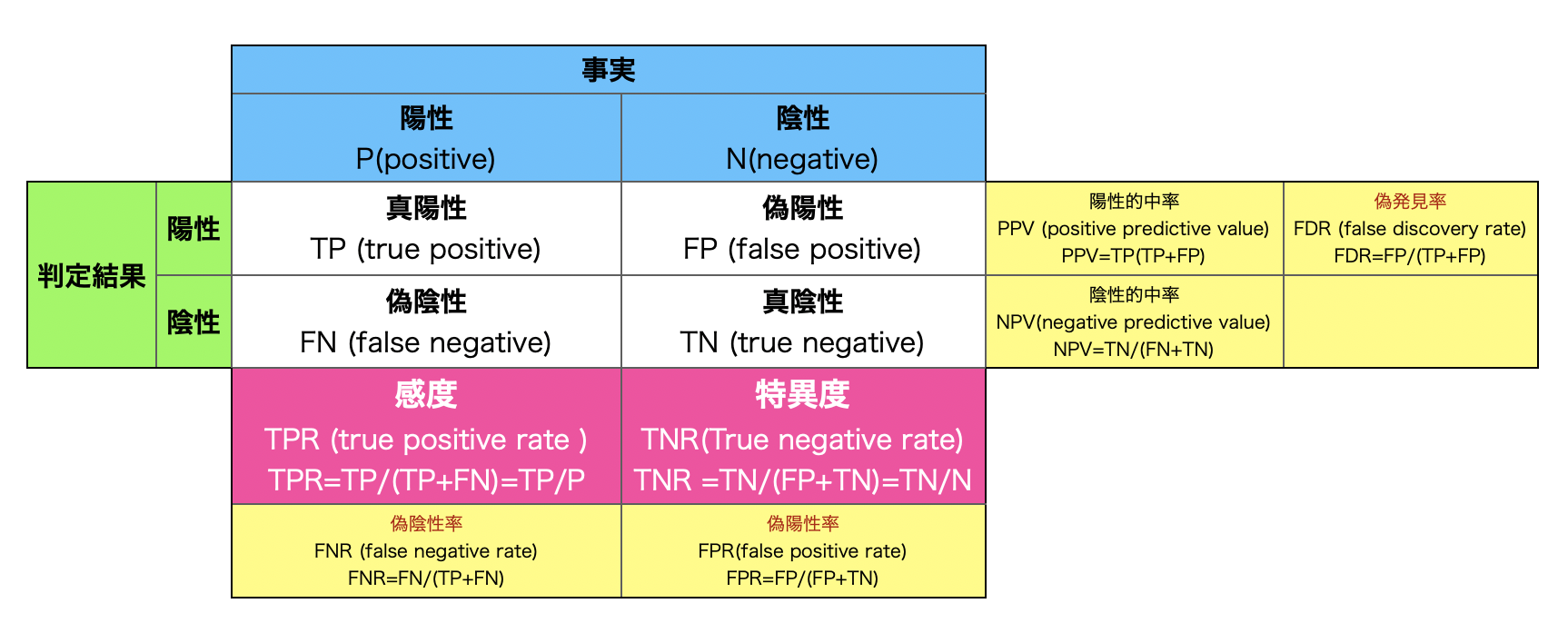
感度 sensitivity

現実に陽性である人が検査で陽性である確率。全ての検査結果を陽性にした場合は感度100％となります。
True positive rate (TPR) とも言います。

TPR=TP/(TP+FN) =TP/P

特異度 specificity

現実に陰性である人が検査で陰性である確率。全ての検査結果を陰性にした場合は特異度100％となります。
True negative rate (TNR) とも言います。

TNR =TN/(FP+TN) =TN/N

実際に検査と同じ判定を機械学習モデルでしてみたとしよう

今話題の新型コロナウイルス感染症（COVID-19）のPCR検査と同程度の精度と考えられる画期的な機械学習モデルがあったとして計算してみましょう。新型コロナウイルス（2019-nCoV）の遺伝子検査法の詳しいデータは見つかりませんでしたが、いくつかの医療関係者の記事などから僕が選んだ値、感度70%・特異度90％と仮定します。

※新型コロナウイルス感染症（COVID-19）のPCR検査のような検査は、検体を採取する時に適切な方法やタイミング、採取環境や検体の取扱いで検査の結果に大きな違いが出るそうです。研究所内で閉じたPCR検査の特異度は95%を遥かに超えるものの実際の検査では異なるようです。今回は計算のしやすさも考慮し便宜的に上記の感度と特異度に仮定しました。

絞り込まれてない大多数という存在

機械学習を利用したい場面では特定の条件にあった人が選ばれる場面とは限りません。
例えば同じ会社の人、今日すれ違った人、SNSの向こう側にいる人から無作為の10000人に機会学習による判定をしてみると仮定します。新型コロナウイルス感染症（COVID-19）の人数は分かりませんが、これも仮に10%(1000人)としてみましょう。

※米国の原子力空母の乗務員4500人中500人以上が新型コロナウイルス感染症（COVID-19）に感染した例を参考にして、有病率(ウィルスの保有者)は10%としています。なおこの空母では感染しているのに無症状だった人は約60％もいたため機械学習による自動判断が行えればとても助かる環境かもしれないと利用しています。

※医療の世界では明らかに疑いがある人に初めて検査をすることが多いようです。こうすることで検査数に対する偽陽性の割合を下げています。

数字から見る真実

問題です。
10000人に判定をした場合、判定結果が陽性だった人のうち実際に新型コロナウィルスに感染している人は何人でしょう。
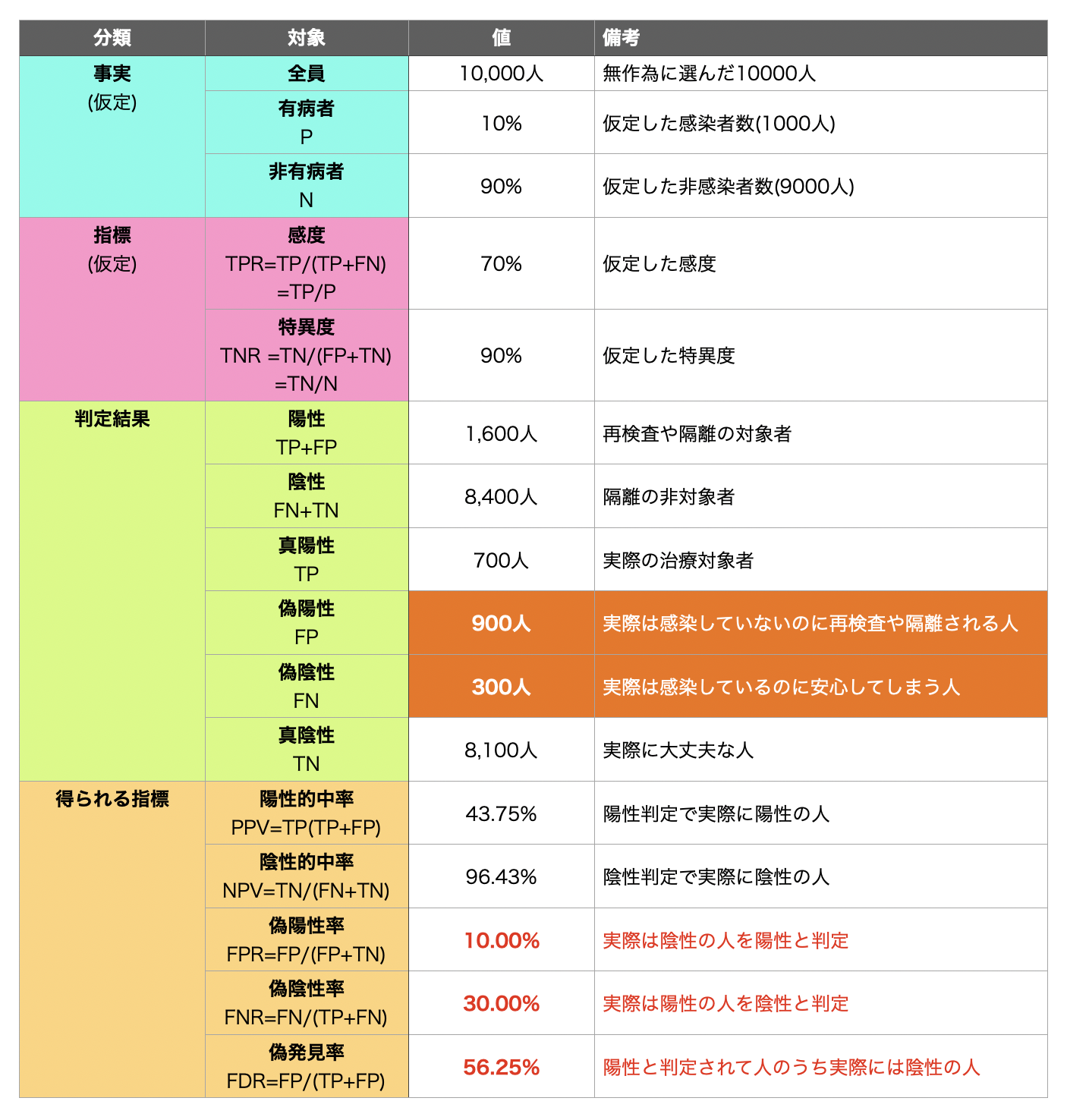
正解は、700人です。

また問題です。
10000人に判定をした場合、判定結果が陽性だった人のうち実は新型コロナウィルスに感染していない人は何人でしょう。
正解は、900人(実に陽性判定者の56%以上)です。

検査結果が陰性だった人が実際に新型コロナウィルスを持っていない場合は8100人と問題ない数字に見えますが、陰性と判断された人で新型コロナウィルスに感染している人は300人(実際に陽性の人のうち30%)もいます。

※無作為ではない人を対象に行われた検査における実際の事象として、愛知県で2020年4月11日に発表した検査結果28人のうち24人を誤って陽性と判定していたことが明らかになっています。この件は検査を依頼した4人全員が陽性になったことに違和感を感じた新城保健所が指摘し発覚しましたが、偽陽性だと明確に発覚することは稀だと考えるべきでしょう。

エンジニアが把握すべき指標

ここからは上記の計算をもとに、エンジニアが常に確認すべき指標で簡単に計算できるものを洗い出してみます。

陽性適中率

検査で陽性だった人が現実に陽性である確率。
positive predictive value(PPV)とも言います。

PPV=TP(TP+FP)

陰性適中率

検査で陰性だった人が現実に陰性である確率である確率。
negative predictive value(NPV)とも言います。

NPV=TN/(FN+TN)

偽陽性率

現実に陰性の人が陽性と判断される確率。
false positive rate(FPR)とも言います。

FPR=FP/(FP+TN) =FP/N

偽陰性率

現実に陽性の人が陰性と判断される確率。
false negative rate(FNR)とも言います。

FNR=FN/(TP+FN) =FN/P

偽発見率

陽性と判断した結果のうち、現実に陰性の人である確率。
false discovery rate(FDR)とも言います。

FDR=FP/(TP+FP)

結果の影響を考えてリリースしよう

今回計算した値やその判定結果に対する表現は新型コロナウイルス感染症（COVID-19）を例に取ったのでかなり厳しくなっていると思います。
しかし、実際に我々エンジニアがユーザーに与える影響を真摯に受け止めるのにはいい機会だと思いました。
本当に画期的な方法でモデルを作成しPCR検査をしなくてもPCR検査と同レベルでの新型コロナウイルス感染症（COVID-19）の人を判定できる空想のモデルを開発したとし、どうリリースすればいいのかを掘り下げて考えてみましょう。

他に方法はあるのか？

例にしている画期的な空想の機械学習モデルで陽性と判定された対象者(上記1600人)が出た場合、多くが実際のPCR検査をしてもらうのではないでしょうか？
しかし今回例にした空想のモデルは実際のPCR検査とだいたい同じ確率なので、PCR検査では陰性と判断される可能性があります。その人は本当に陽性なのか陰性なのかわからずじまいです。
また、陰性だった人に再検査を促す道はあるのでしょうか？

無駄に不安を煽るべからず

新型コロナウイルス感染症（COVID-19）について様々な知識を得ているエンジニアはCTを撮ることで特徴的な肺炎から真実がわかると考えかもしれません。
しかしCTでわかるのは肺炎が起こったあとです。肺炎を起こす前に不特定多数に使った場合、陽性と判定された人の運命はどうなるのでしょう？
無症状の人だったとしても周囲の人を含めた不安はかなり大きなものではないでしょうか？

無駄な安心を与えるべからず

新型コロナウイルス感染症（COVID-19）を例にとった場合、一番最悪のシナリオはこのパターンかもしれません。
無症状だったり軽症たっだ人が陰性の判定を受けた結果、再び公共交通機関で出勤し、スーパーで買い物をして他者を感染させ続けてしまいます。
多くの人は加害者になりたくないと考えられるため、このような結果を望んで判定や検査をしている人はいないのではないでしょうか？

判定結果を最後に受けるのは人間

エンジニアは最終的に人が関わる問題をテクノロジーとエンジニアリングで解決するのが仕事です。
ですから、優秀なモデルを開発しただけでは不十分で、この現実世界で便利に使えることで初めて解決したと胸を張れると僕は考えています。

例えば空想のモデルをもし肺炎の症状がある人に使えばPCR検査よりも高速で一次判定ができPCR検査よりも数がこなせる機械学習モデルは非常に役立つでしょう。
また都度都度の判定結果を公表せず、同じ人が生活する中で何か特別な行為をしなくても、何度も何度も機械学習による判定を自動的に受けれるようにすることで、結果的に正しい判定結果に近づけていき一定の閾値を超えた時点で適切に体調に関するアンケートを通知する仕組みがあれば肺炎になる前に利用できるかもしれません。

そのように、役に立って初めて現実社会でエンジニアリングの価値が生まれます。