2度目まして！22年度新卒入社いたしました、三瀬 リキトと申します。

この度機会をいただけましたので、僕が学生時代に一生触れてきた技術(?)をわかりやすく紹介していきたいと思います。

僕は高専の卒業研究で、「カオスなセル・オートマトンによる暗号作成」というテーマで研究を行ってきました。

この研究の本質は暗号作成の部分なのですが、今回は「セル・オートマトン」という数理モデルについて興味を持っていただけたらなと思い、執筆しました。

①セル・オートマトンについて　

セル・オートマトンは、かみ砕いて言うと「何かしらのルールに従って、一生値が変化し続ける空間」です。人生のようなものですね。

「空間」とは、マス目のようなもの(英語でセルと呼びます)に、「状態」と呼ばれる何かしらの値がそれぞれ入っているもので、その空間は一次元でも二次元でも三次元でも大丈夫です。

僕の研究では、一次元の空間を扱っていたので、今回は一次元でのセル・オートマトンを紹介していきます。

例えば、以下のような一直線に部屋が並ぶアパートがあったとします。

前提として、この部屋の住人は全員20歳以上であり愛飲家であるとします。

この部屋の住人は、偶然以下のような規則性で飲酒をしていました。

　・両隣の部屋が片方だけ飲酒をしていたら、次の日飲酒をする
　・両隣の部屋が両方飲酒をしていなかったら、次の日飲酒をしない
　・両隣の部屋が両方飲酒をしていても、次の日飲酒をしない

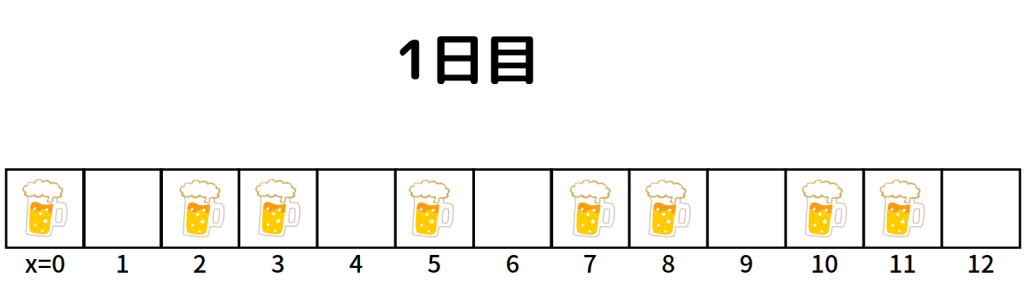
とある日の、各住人の飲酒状況は以下のようでした。この日を「1日目」とします。

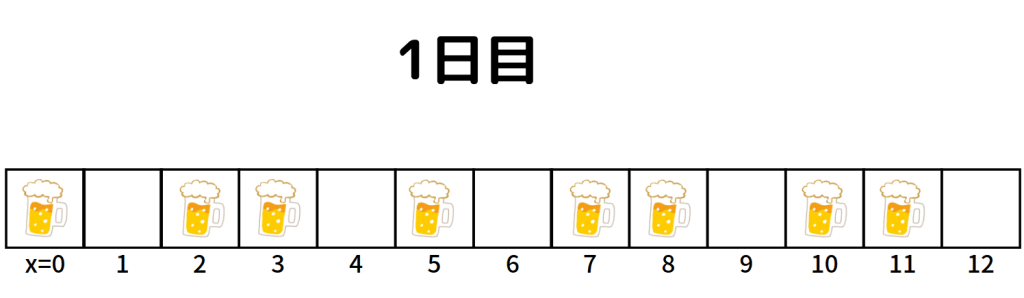
皆まばらに飲んでいたり飲んでいなかったりしますね。この1日目のそれぞれの状況を「初期状態」と呼んでいきます。また、今回は隣が存在しない部分(部屋番号0の左隣の部屋と、12の右隣の部屋)は飲酒をしていない扱いとします。

さて、1日目を終えました。部屋番号0の人は、両隣とも飲酒をしていなかったので、上記の規則にしたがって2日目は飲まないことにしました。これを部屋番号1～12の人も同じようにチェックしていきます。

その結果、2日目は以下のようになったと思います。

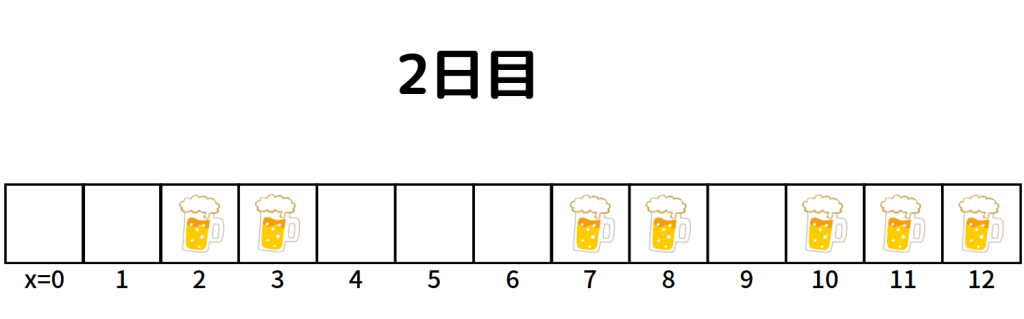
規則性によって、2日目も飲酒をする人/しない人がそれぞれ決定されましたね。

どんどんこの規則にしたがって日を進めていきましょう。

3日目です。

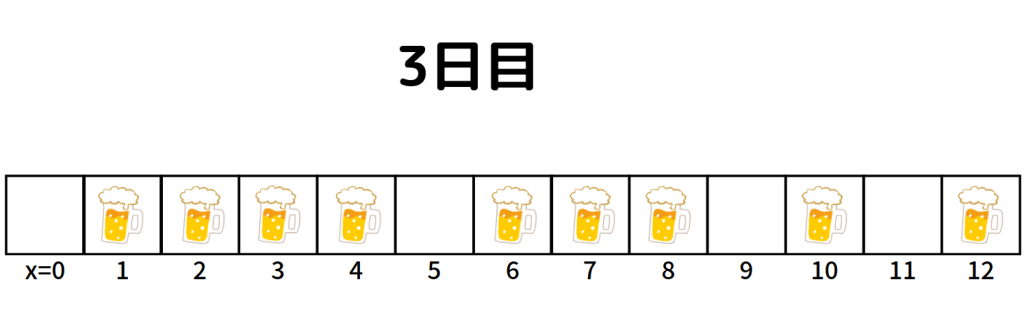
4日目です。

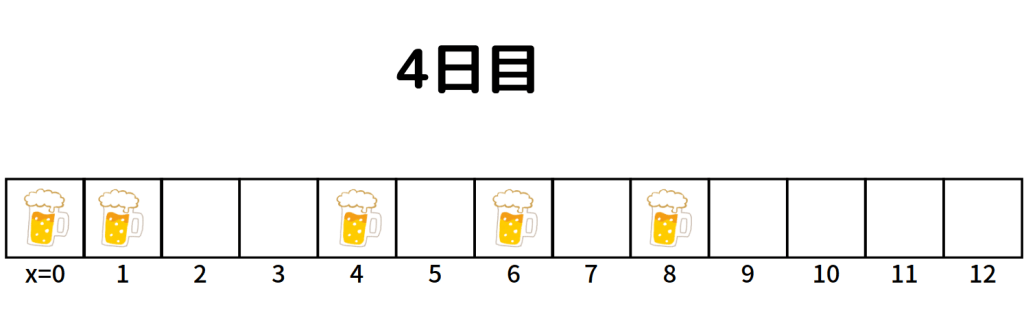
これ以上やると、くどくなってしまいますね。

ですが、お分かりいただけたでしょうか。この部屋の住人は、1日目の「初期状態」と最初に定めた「規則」によって、外から一切手を加えることなく何日も飲酒/非飲酒を決定していきました。もちろん、この先もずっとです。

また、この飲酒を「1」、非飲酒を「0」とすると、4日目は以下のようになります。

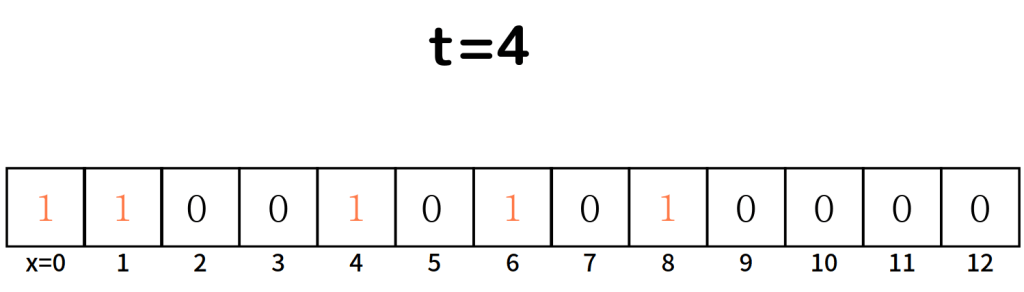
ちゃんと数理モデルっぽくなりましたね。これがセル・オートマトンです。

このように、セル・オートマトンは、最初に僕たちが「初期状態」と「規則」さえ決めてしまえば、あとは勝手に、無限に状態変化を続けてくれるのです。無限にです。

また、この例では状態が「飲酒」「非飲酒」だけなので「0」か「1」の2つになりましたが、この数字が3つでも4つでも、それに合う規則さえ設定すれば大丈夫です。

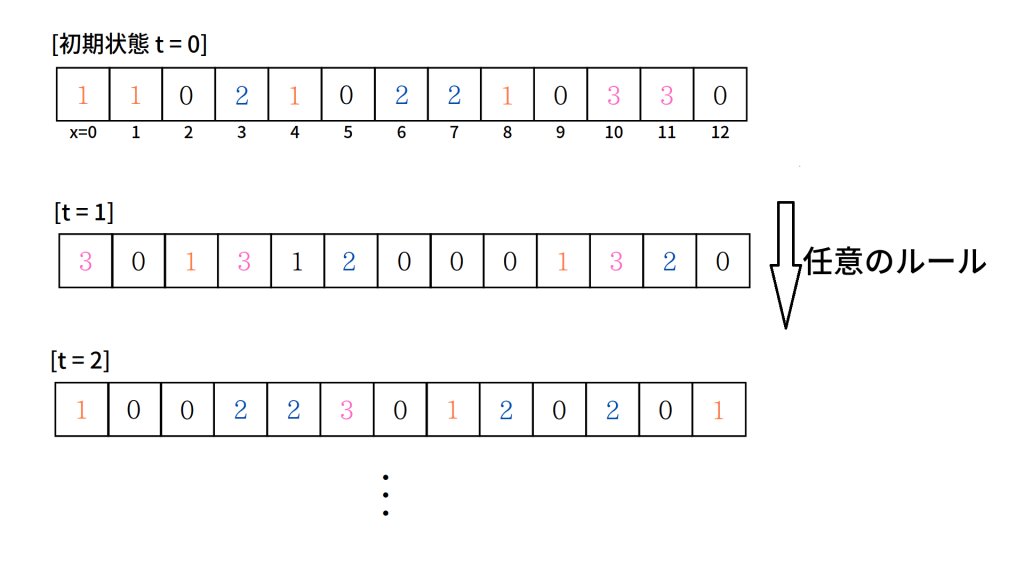
少々、興味を持っていただけたでしょうか？

これからもっと興味を持っていただきたいので、僕が研究で扱った「カオスなセル・オートマトン」について簡単に説明していきたいと思います。

②カオスなセル・オートマトンについて

カオス（英: chaos）またはケイオスとは、「混沌」を意味する英語である。無秩序で、さまざまな要素が入り乱れ、一貫性が見出せない、ごちゃごちゃした状況・様相を形容する表現として用いられることが多い。

カオスとは何？Weblio辞書

①で紹介したようなセル・オートマトンの規則は、何日も続けていたら周期的に同じような状態の組み合わせが出てきたりします。

カオスなセル・オートマトンとは、何日続けていても同じような状態の組み合わせが出てこない規則のことを指します。今回は、そのカオスな規則として「ルール30」という規則を紹介します。

ルール30は、①で紹介した規則と同じ一次元セル・オートマトンで、しかも状態も「0」か「1」のどちらかです。

つまり、先ほどのお酒の例が使えるということですね！！

ということでお酒の例に照らし合わせると、ルール30の規則は以下のようになります。

　・自分が飲んでいなくて、両隣も飲んでいなかったら、次の日も飲まない
　・自分と左隣が飲んでいなくて、右隣だけ飲んでいたら、次の日は飲む
　・自分が飲んでいて、両隣が飲んでいなかったら、次の日も飲む
　・自分と右隣が飲んでいて、左隣だけ飲んでいなかったら、次の日も飲む
　・自分と右隣が飲んでいなくて、左隣だけ飲んでいたら、次の日は飲む
　・自分が飲んでいなくて、両隣は飲んでいたら、次の日も飲まない
　・自分と左隣が飲んでいて、右隣だけ飲んでいなかったら、次の日は飲まない
　・自分が飲んでいて、両隣も飲んでいたら、次の日は飲まない

ゲシュタルト崩壊するくらいややこしいですね。文章にするとあれなので、順番そのままで数値的に示すと以下のようになります。

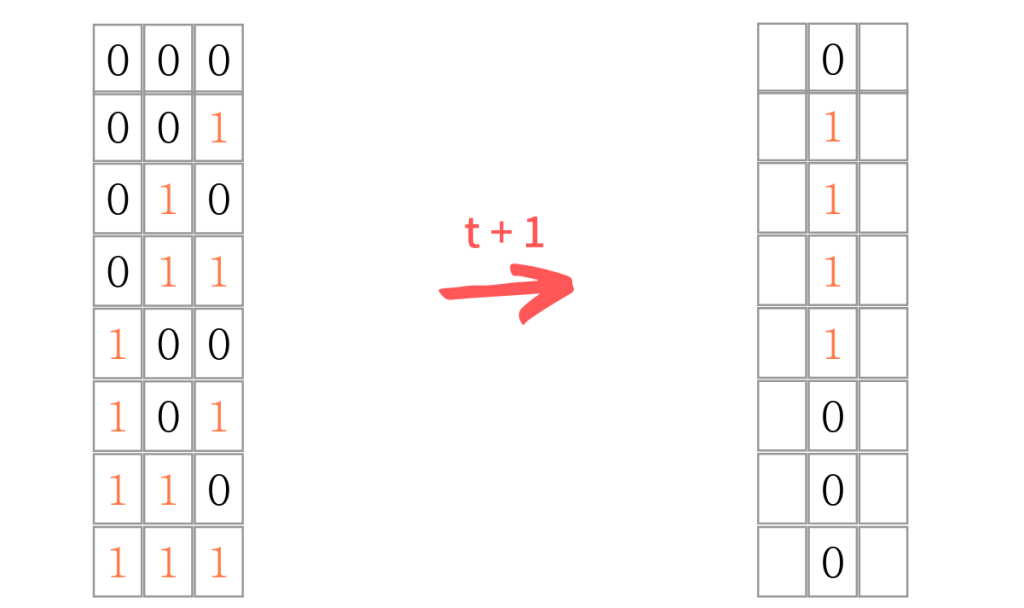
数値で示すとわかりやすいですね。この↑の図の右側の数列を右回転させると「00011110」となって、十進数で30なので「ルール30」と呼ばれています。

余談なのですが、①で紹介した規則は同じように「ルール90」と呼ばれています。どうしてそうなるのか、同じように考えてみてください！！

さて、せっかくなのでルール30でも同じようにお酒の例で更新させてみましょう。

1日目を「初期状態」として、これにルール30という「規則」を適用させると、2日目は

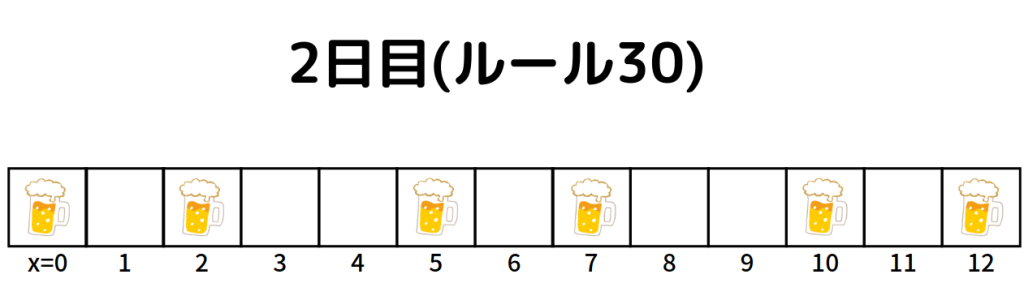
こんな感じになります。

ただルール30の規則はたった8パターンと単純だし、この例ではこのルールが「カオス」なのかどうかは分からないですね。。。

結論から言うと、ルール30はとある外国の学者によって「カオス性」が証明されたものです。

どんな感じにカオスなのか、視覚的にわかりやすいように過去にプログラムでシミュレーションを行った画像を使ってご紹介します。

まず、以下の画像はカオスではない規則「ルール90」の状態変化の様子をシミュレーションしたものです。

この図は「0」を白「1」を黒として、初期状態を真ん中だけ「1」他は「0」にして(ピラミッドみたいになってるやつの山頂の部分です)、ルール90を適用した結果を下に下にとどんどん描画していったものです。

最悪この図はよく分からなくても構いません。カオスではないルールだと結構規則的な図ができあがったな～ということだけ覚えていただければ大丈夫です。

さて、カオスと言われているルール30で同じことをしたらどうなるのでしょうか。

結果は以下のようになりました。

ﾜｯ...！

見るからに混沌ですね、まばらに三角形のようなものができていますが大小は異なっています。

ルール30はルール90と同じ8パターンだし単純な処理で扱うことができるのに、なぜかこういった非周期的な状態変化が続きます。どうしてこうなるのか、僕は知りません。

このカオスなルールを利用すれば何ができるかと言うと、見かけ上ランダムな乱数を生成することができます。しかも、「初期状態」と「規則」を設定するだけで無限に乱数を作ってくれるのです。

それはブロック暗号(暗号技術の一種)において、とても使えるのでは？？？となって、ルール30による暗号作成の研究が始まるわけですが、それはまた別の話で。

③まとめ

今回紹介したのは一次元セル・オートマトンですが、二次元セル・オートマトンだと有名なものに「ライフゲーム」というものがあります。楽しいので是非検索してみてください。

僕は情報系の学生だったのですが、数学者の研究室でこういった研究をやっていたため、FIXERでの業務内容は全くの畑違いとなると思います。

ですがこういった研究をやっていたおかげで論理的な思考はかなり身に着けておりますので、バシバシ活用していきたいです。