解けましたか...？

ずばり、あなたが考えているアルゴリズムは...

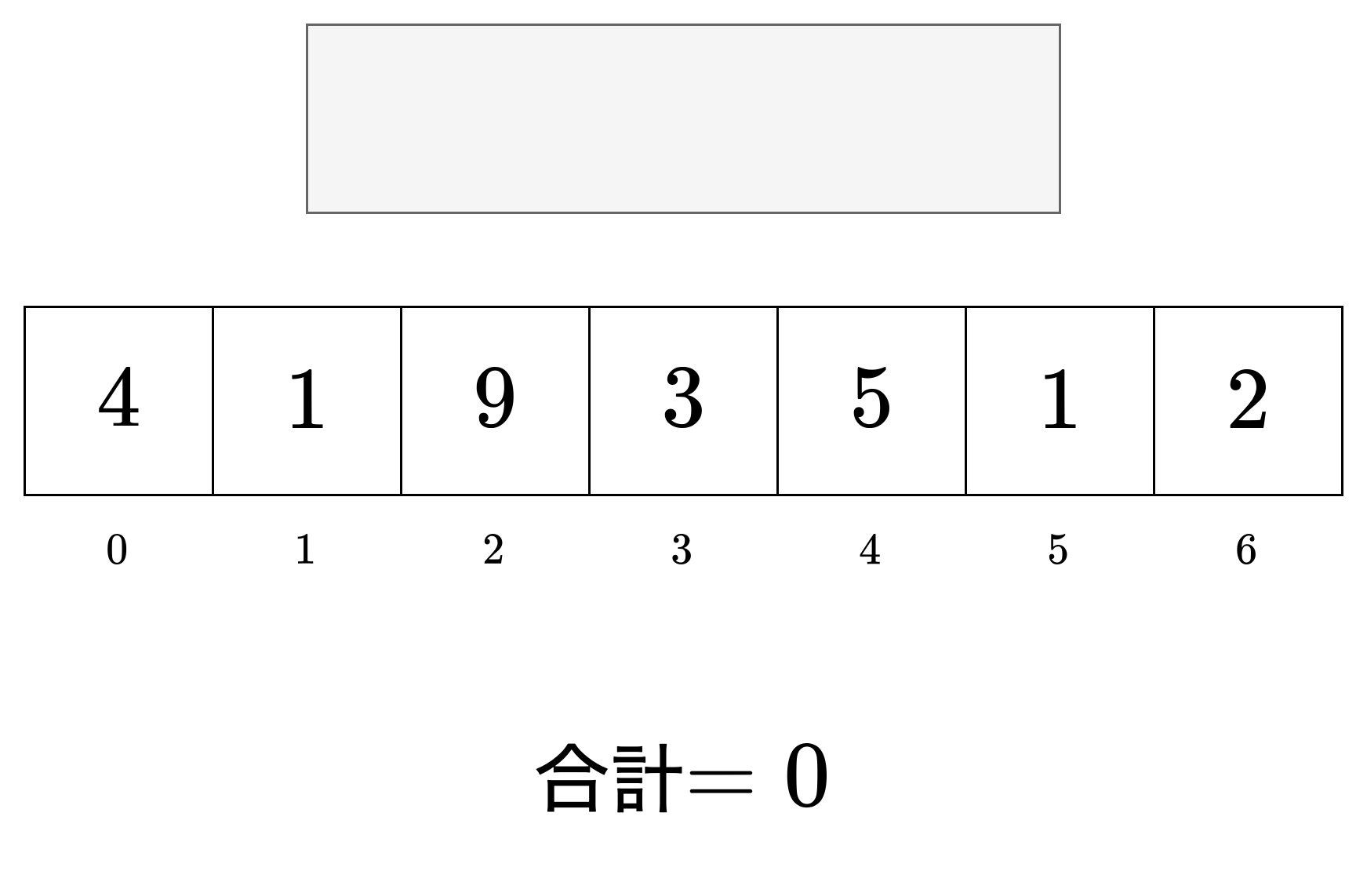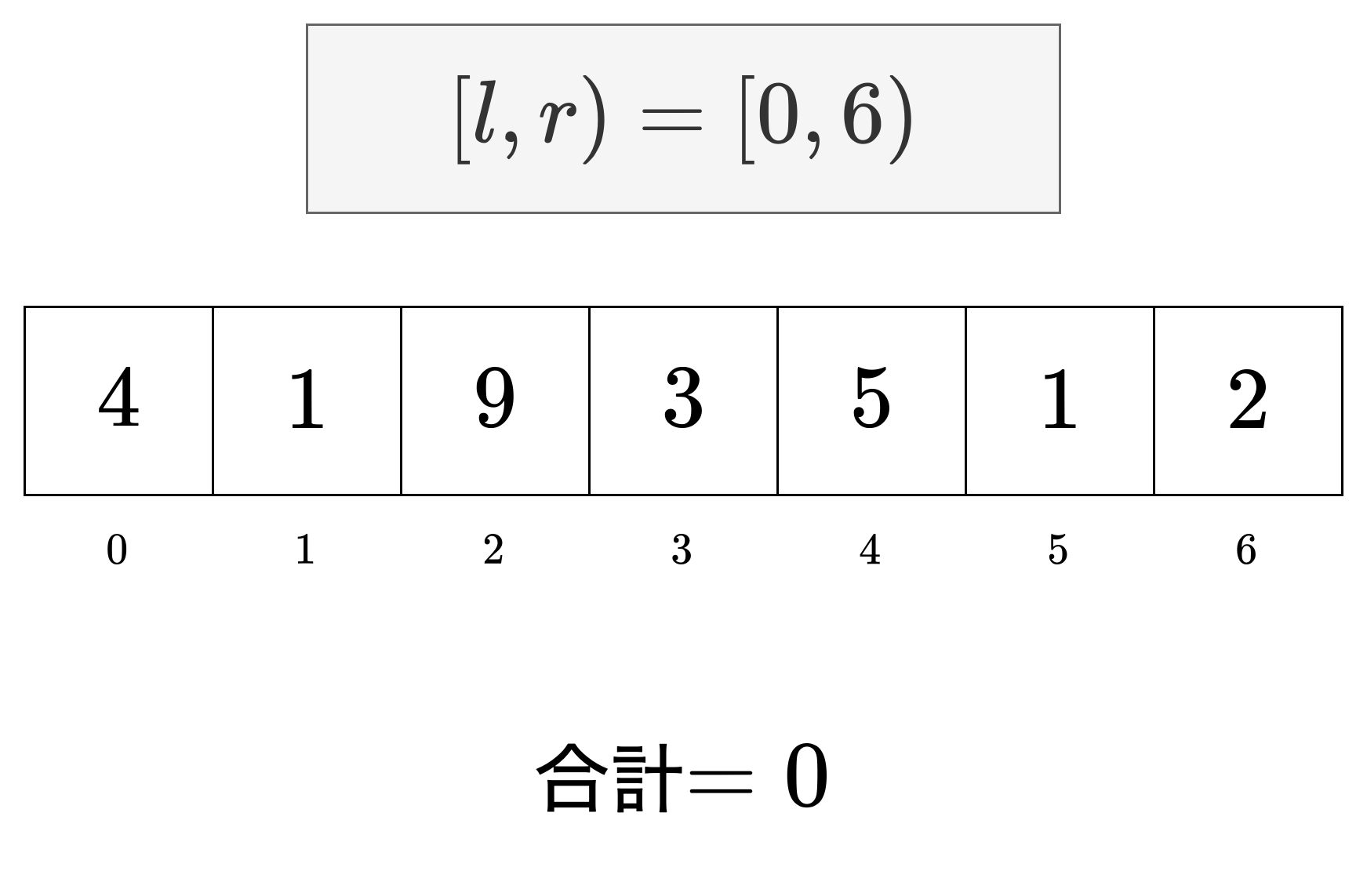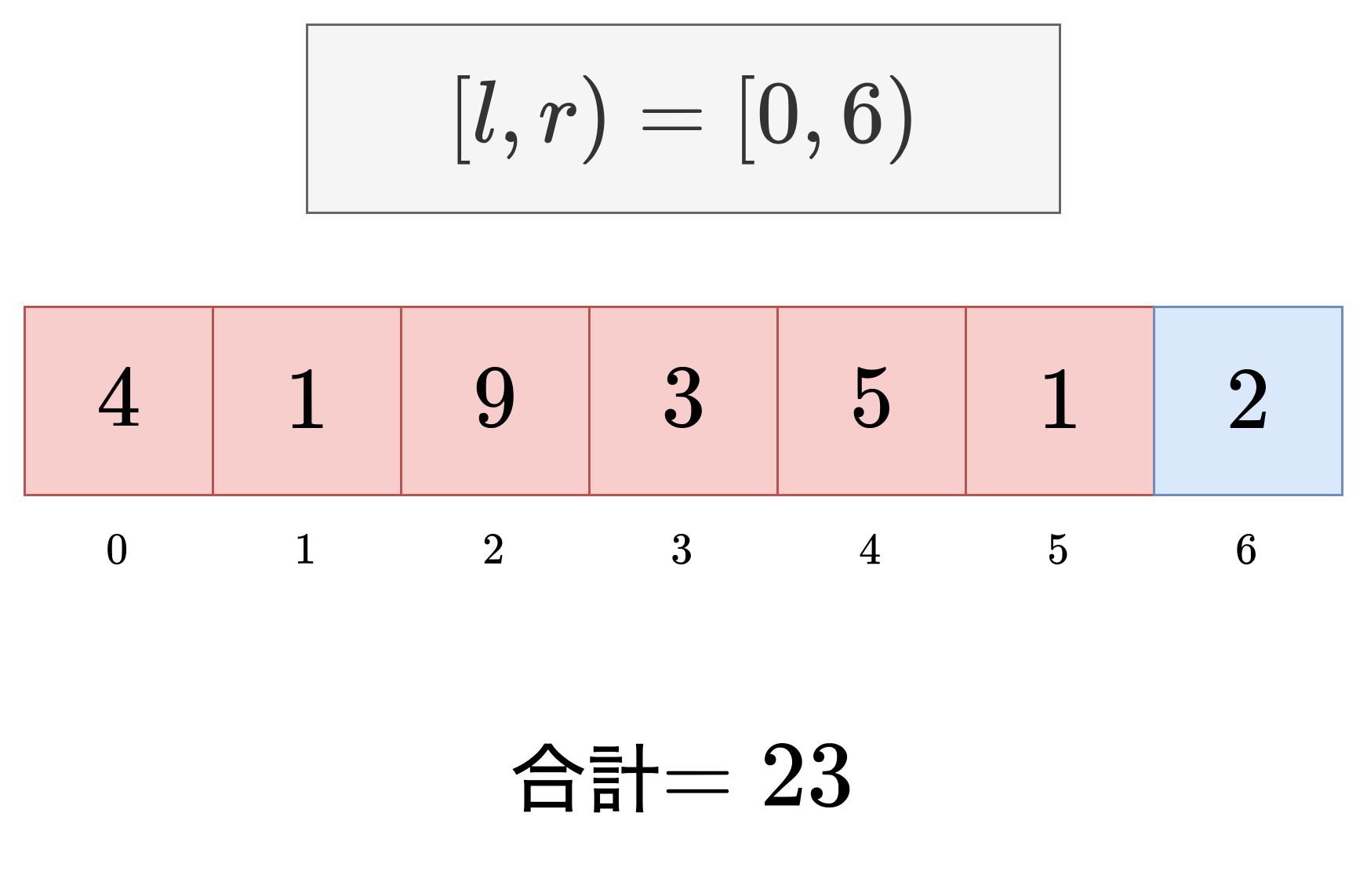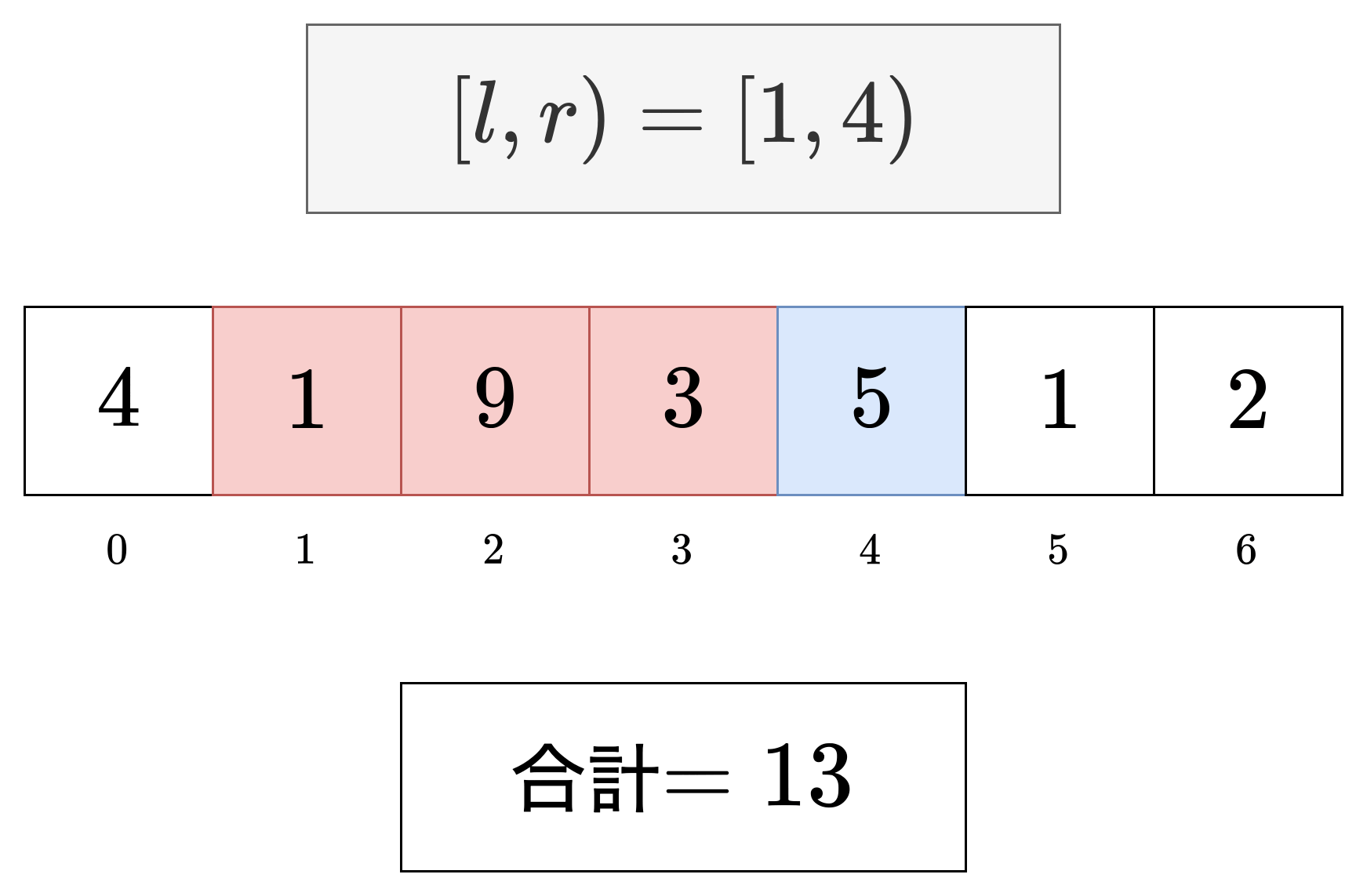
これですね？
C言語で書くとしたら


int calc_sum(int *a, int l, int r) {
	int i, sum = 0;
	for (i = l; i < r; ++i) {
 		sum += a[i];
	}
	return sum;
}

こういうコードになりますね。正解です！
実は、この問題は累積和というテクニックを使えばもっと高速に解くことができます。

累積和ってなに

配列の 前から合計を取ること を累積和といいます。
前処理として累積和の配列を作っておくことで、計算が高速になります。

このGIFのように累積和は簡単に作れます。

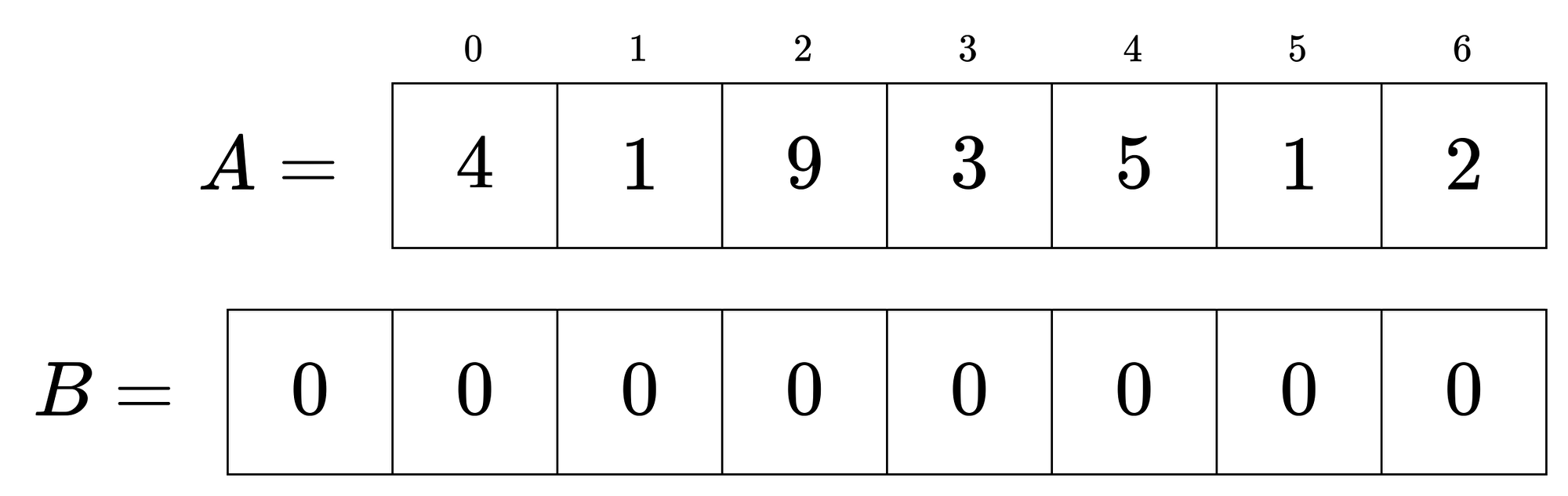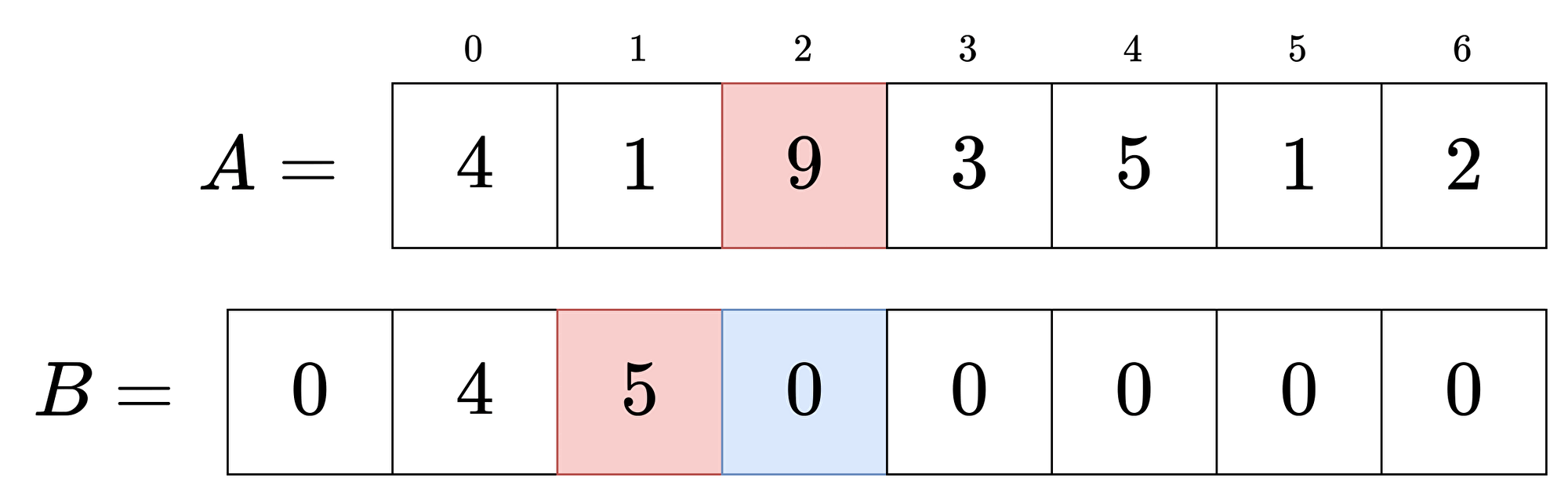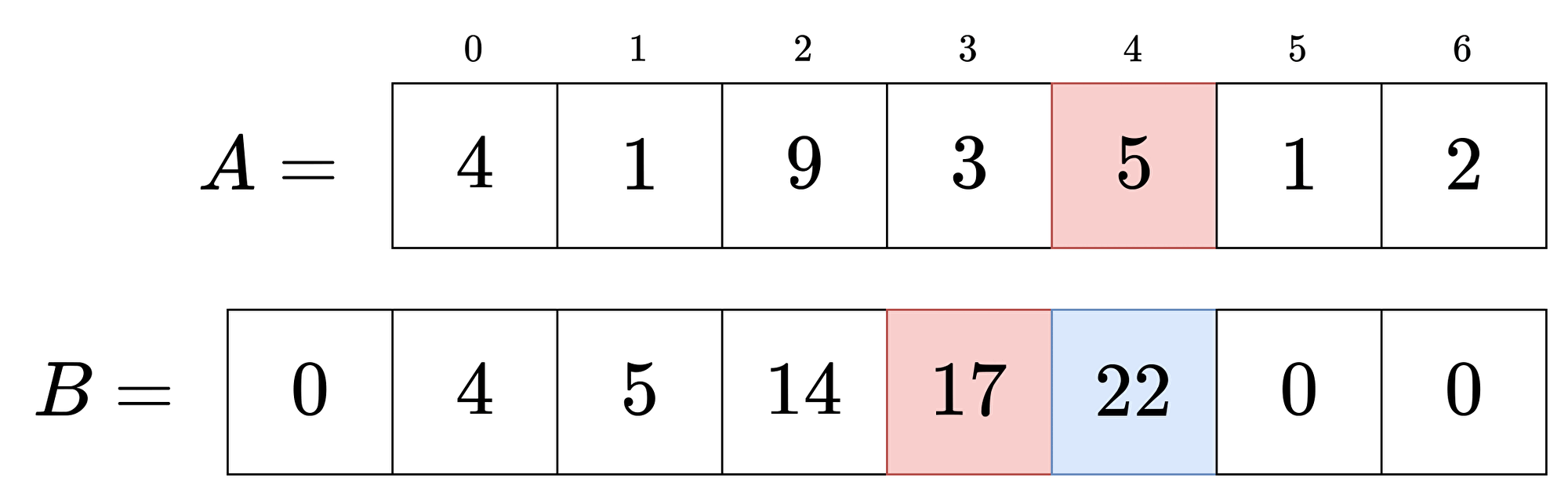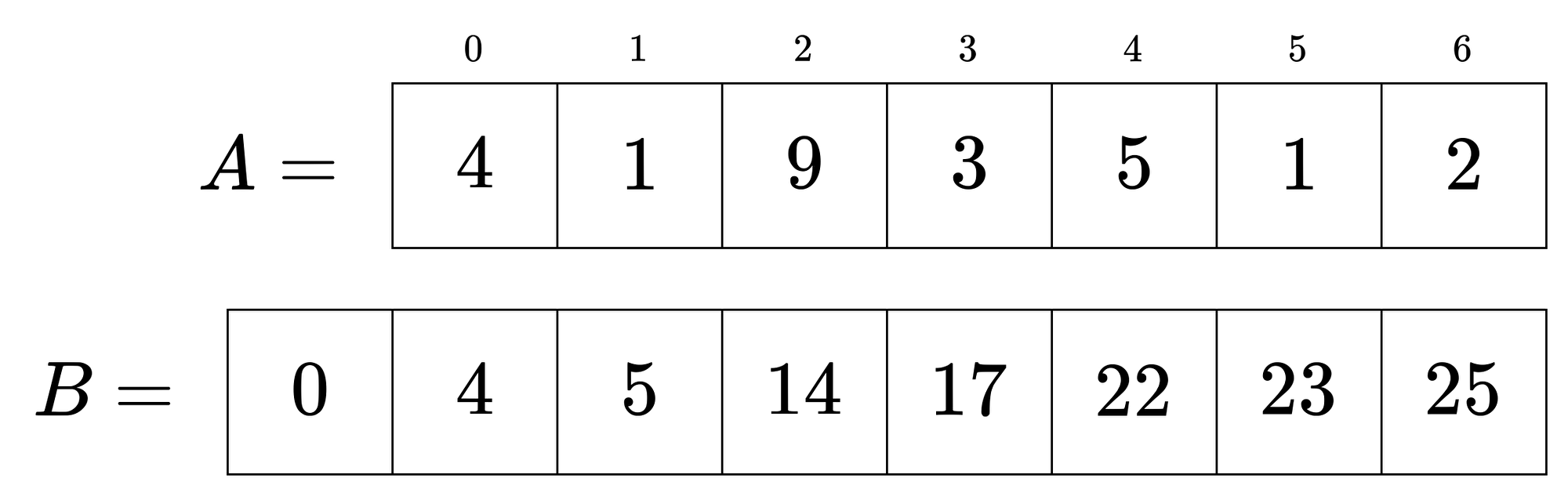
累積和の配列を使えば、元の配列の区間和を1回の計算で求めることができます。
例で使い方を見てみましょう。

例

例として[2,5)を考えてみましょう。

結論から言うとB₅-B₂をするだけで、元の配列の[2,5)の和が得られます。

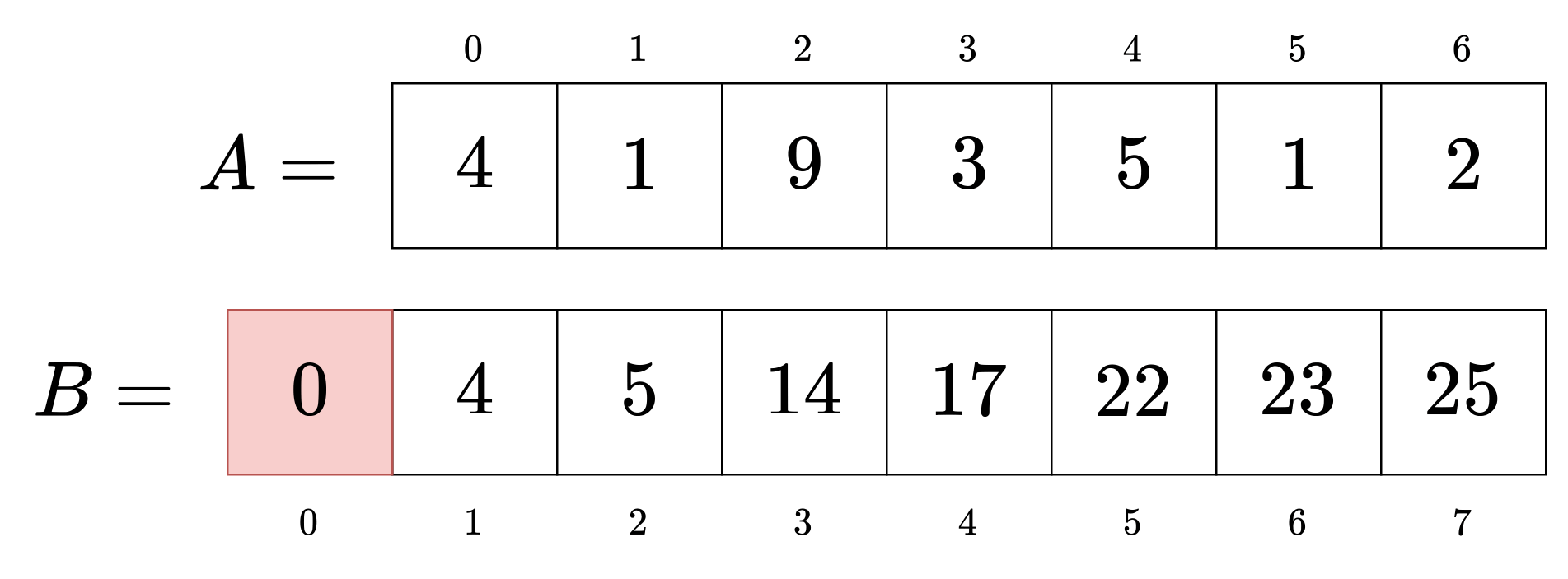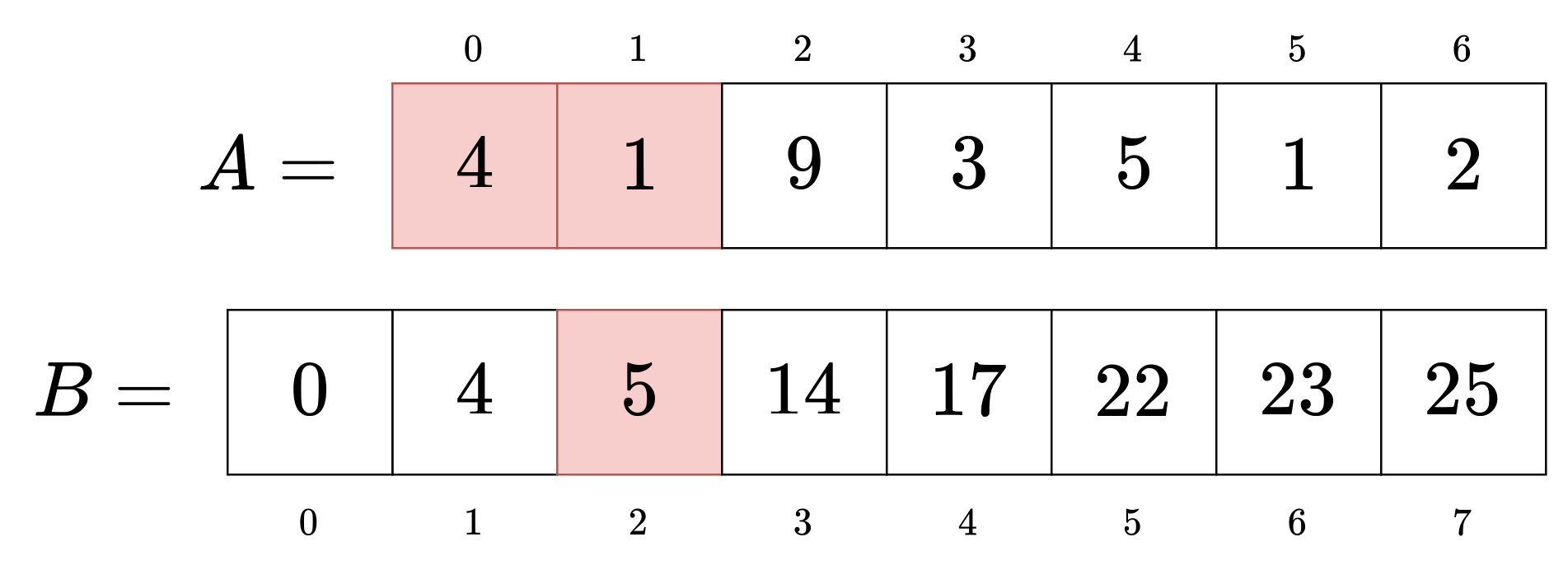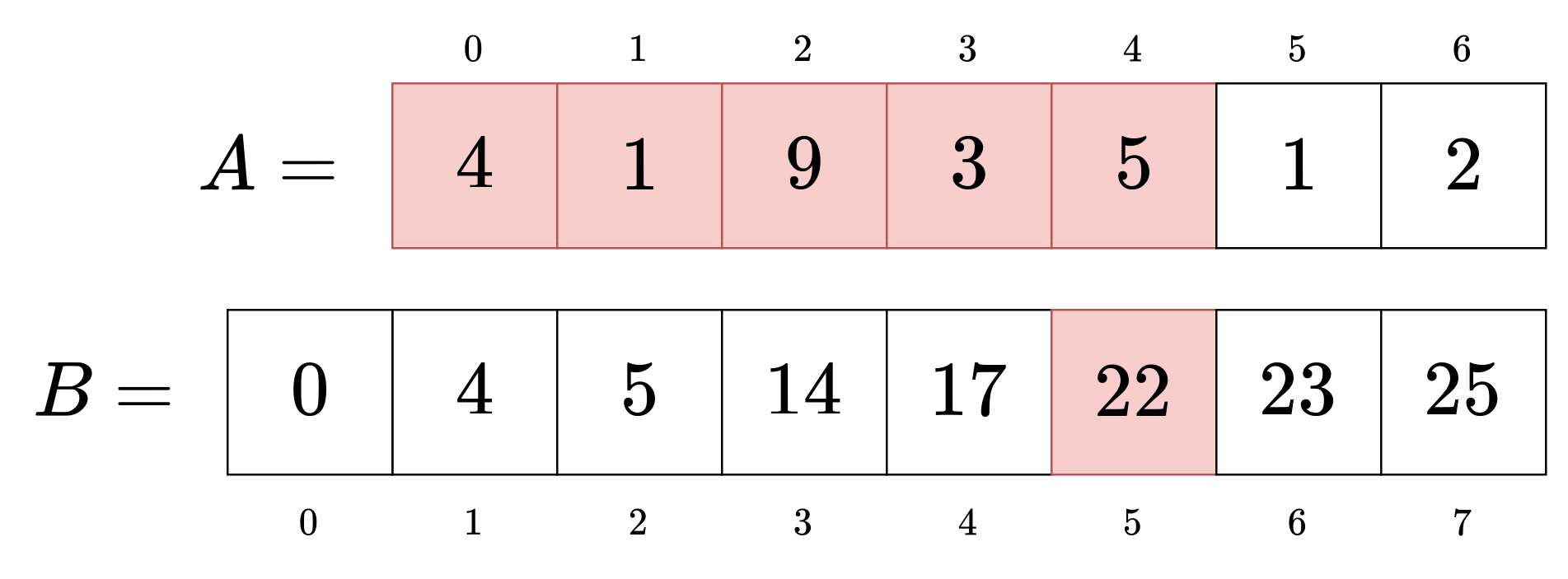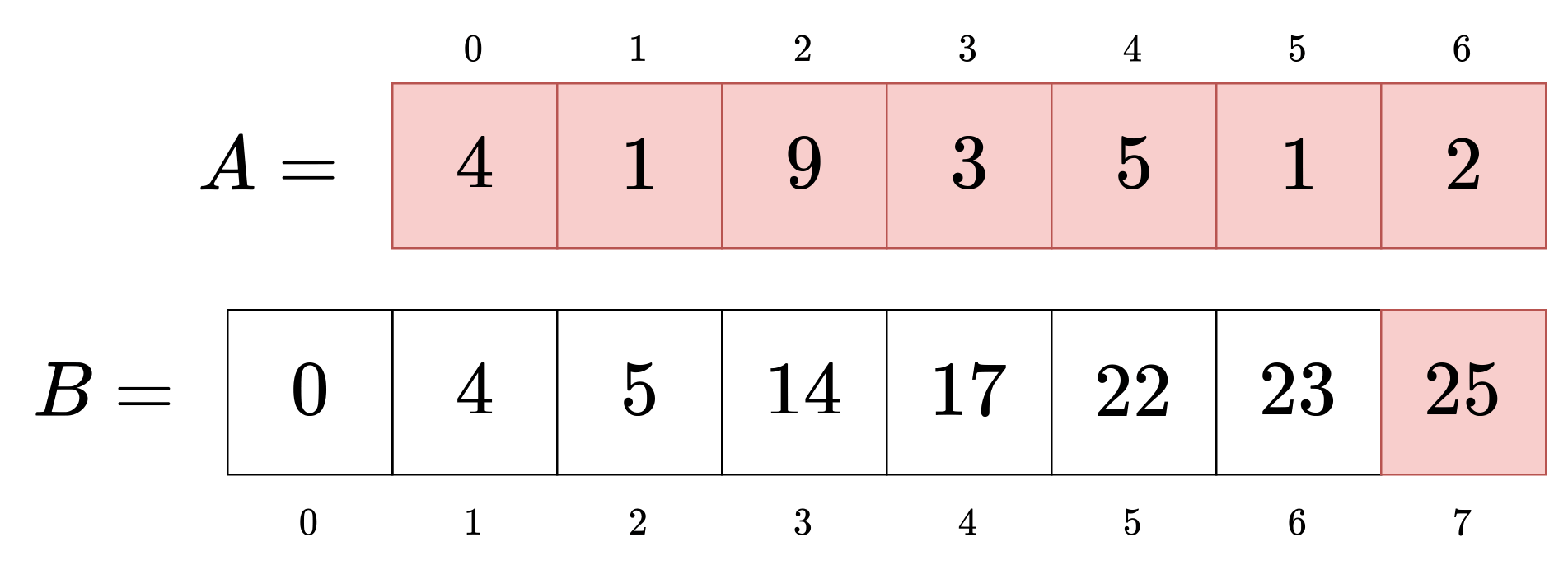
この関係をイメージするとわかりやすいです。

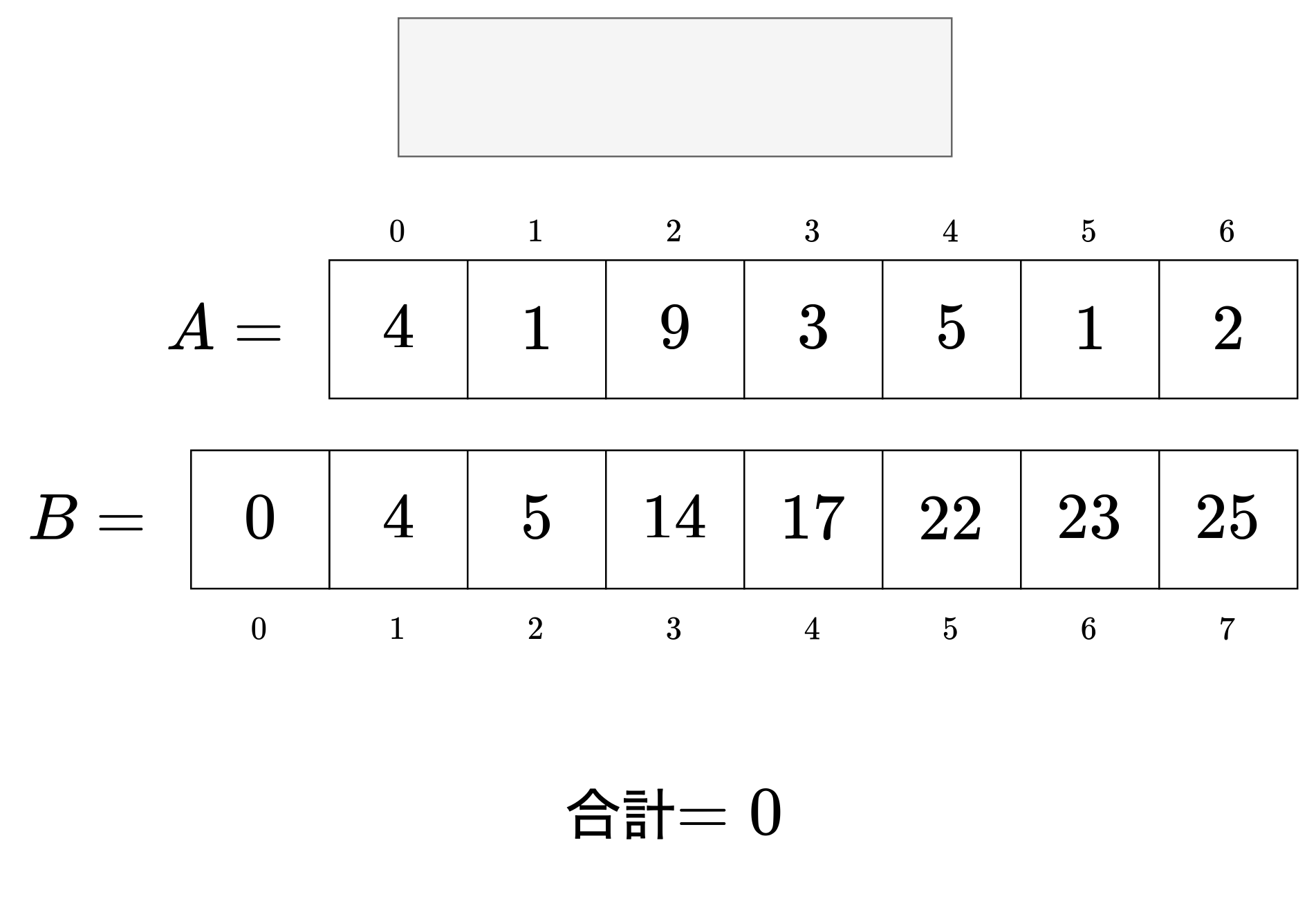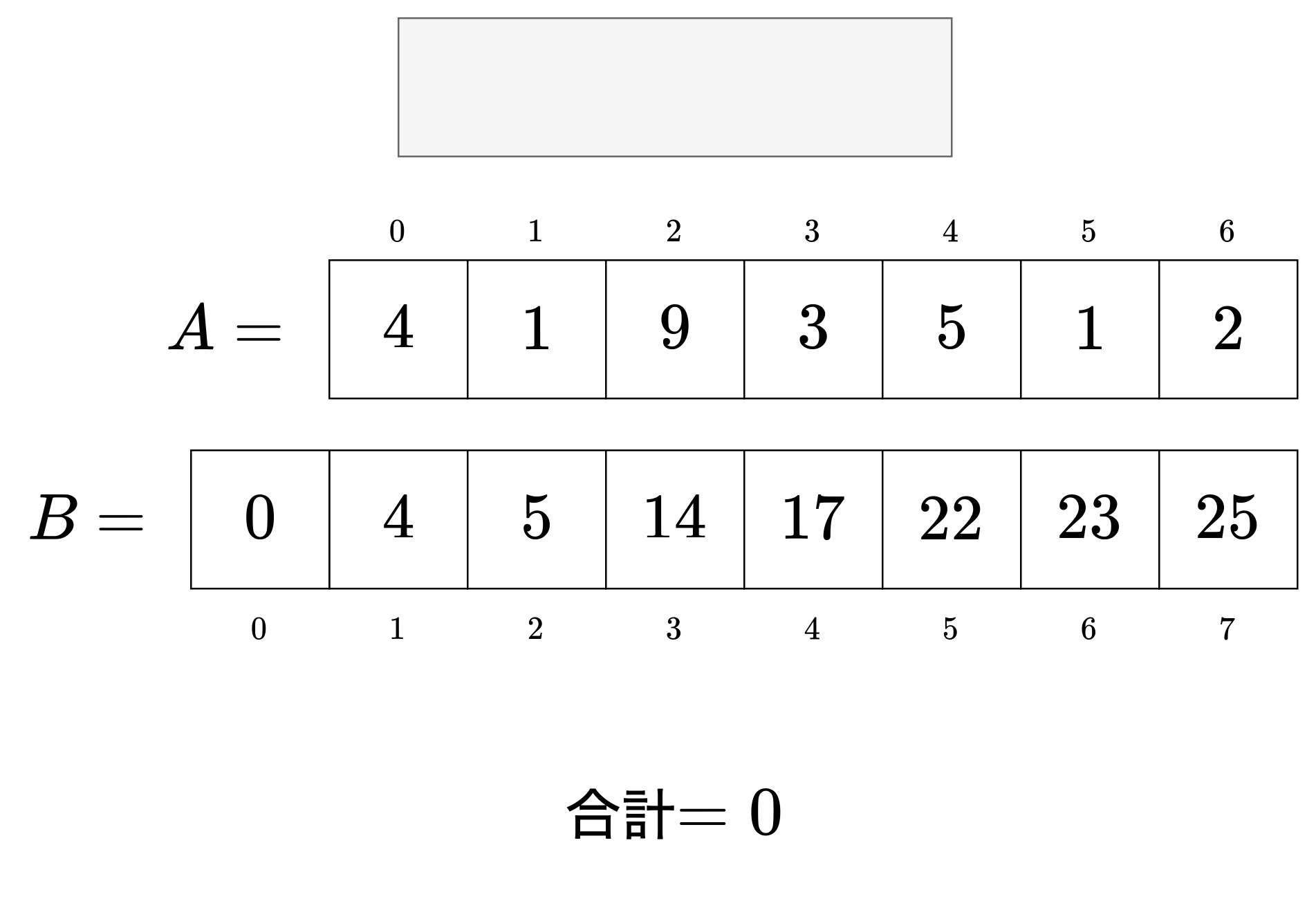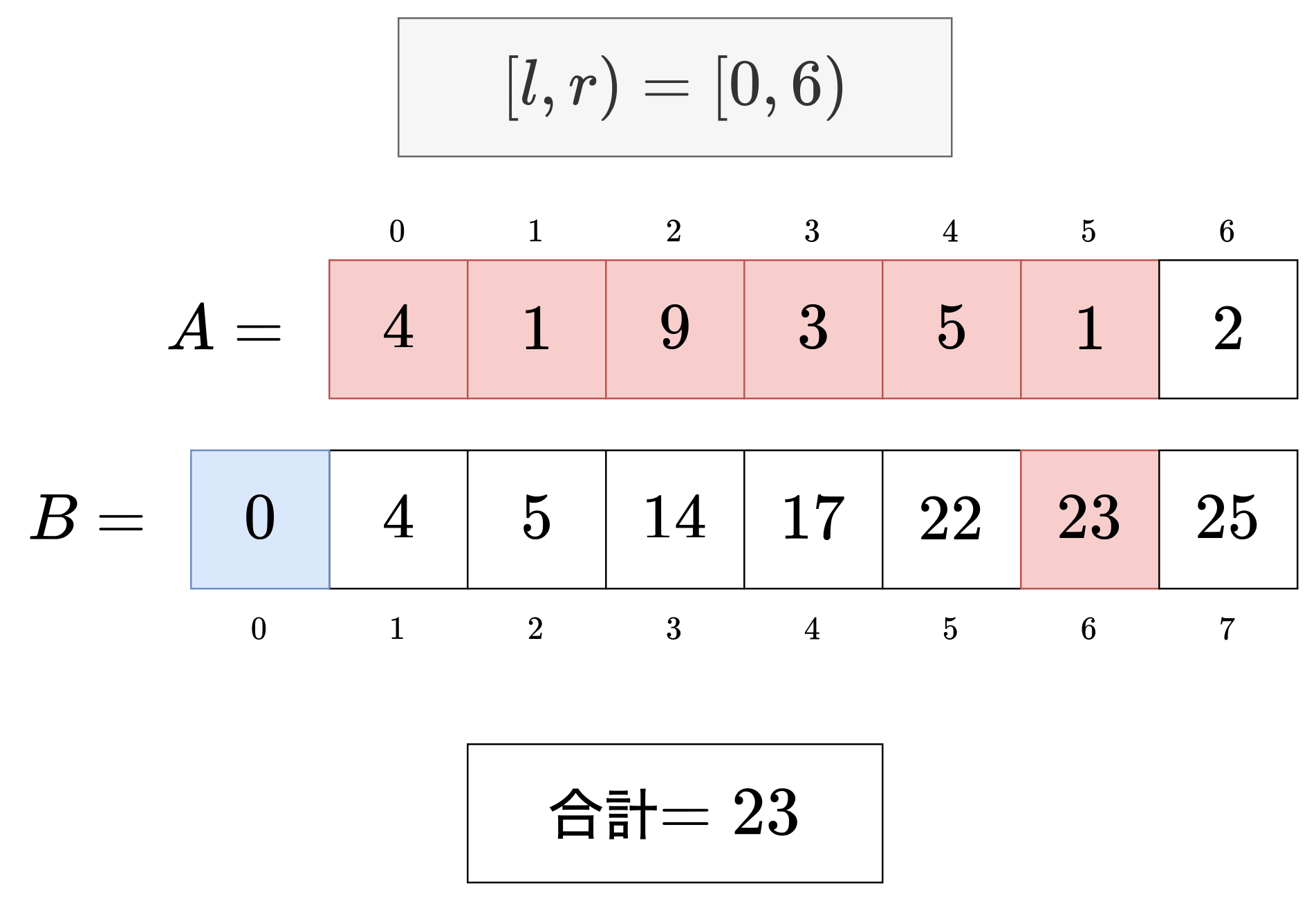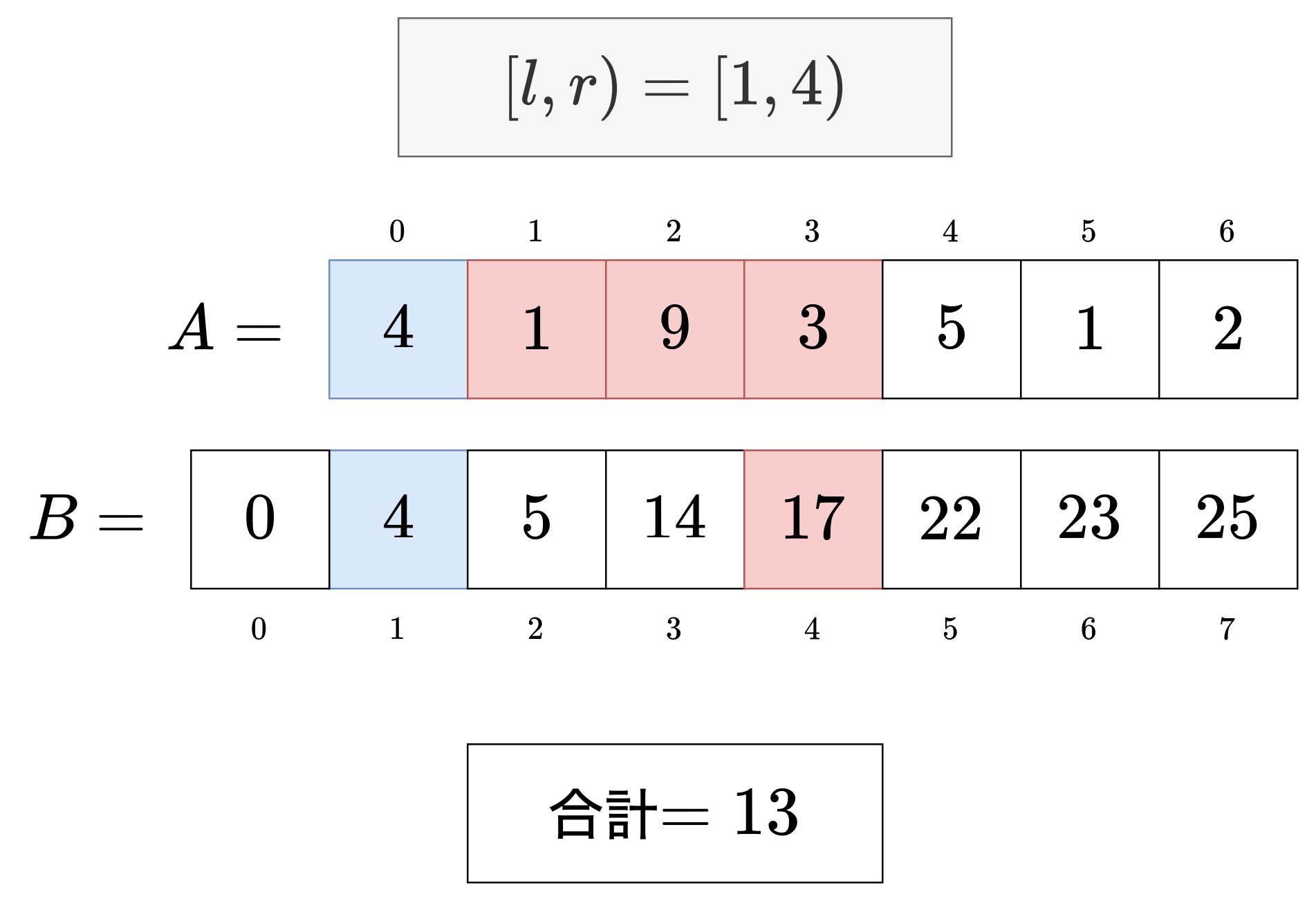
このように1回の計算で区間和を求めることができます。

配列の大きさをN、質問の数をQとして、最悪計算量を計算してみます。

元のアルゴリズムでは、質問される区間がすべて[0,N)の場合が最悪になります。
1つの質問に答えるのに最悪N回計算が必要なので、元のアルゴリズムでは最悪NQ回の計算が必要になることがわかりました。

累積和を使ったアルゴリズムでは、質問される区間に関わらず、2回の計算で質問に答えることができます。
累積和の配列を作るのにN回計算が必要なので、累積和を使ったアルゴリズムではN+Q回計算が必要になることがわかりました。

質問の数が少ないときは累積和を使わないアルゴリズムの方が計算回数が少ないですが、質問の数が多い時に累積和を使うと圧倒的に効率的になります。

配列の長さNを100で固定して最悪計算量をグラフで比較してみます。

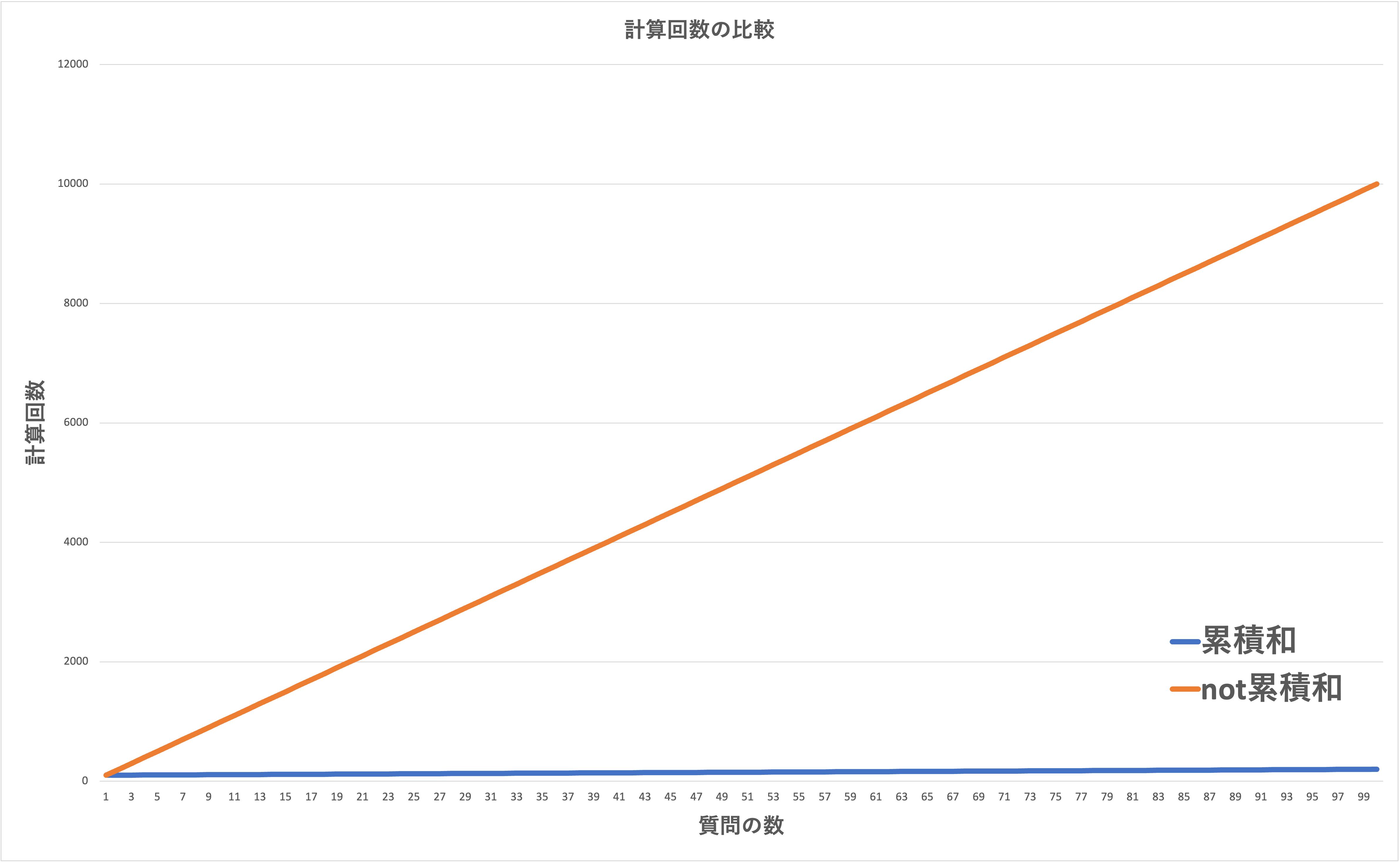
速い！！！！！！！

いかがでしたか？
シンプルなアルゴリズムの改善で劇的に計算回数が変わるの、すごくないですか？

累積和は競技プログラミングの基本テクニックです！
いもす法や動的計画法の高速化、二次元に拡張した二次元累積和など応用の幅は広いので、累積和を習得するだけで解ける問題の幅が広がって競技プログラミングが楽しくなります！！