こんにちは。R&D Divisionの山本です。

今回の記事はコードを書かずに機械学習をしてみよう！の続きとなります。

さて、前回はモジュールを繋げて実行する手順を解説をしましたが、今回は各モジュールで何をしているかを解説していきます。

前回作ったものは以下になります。

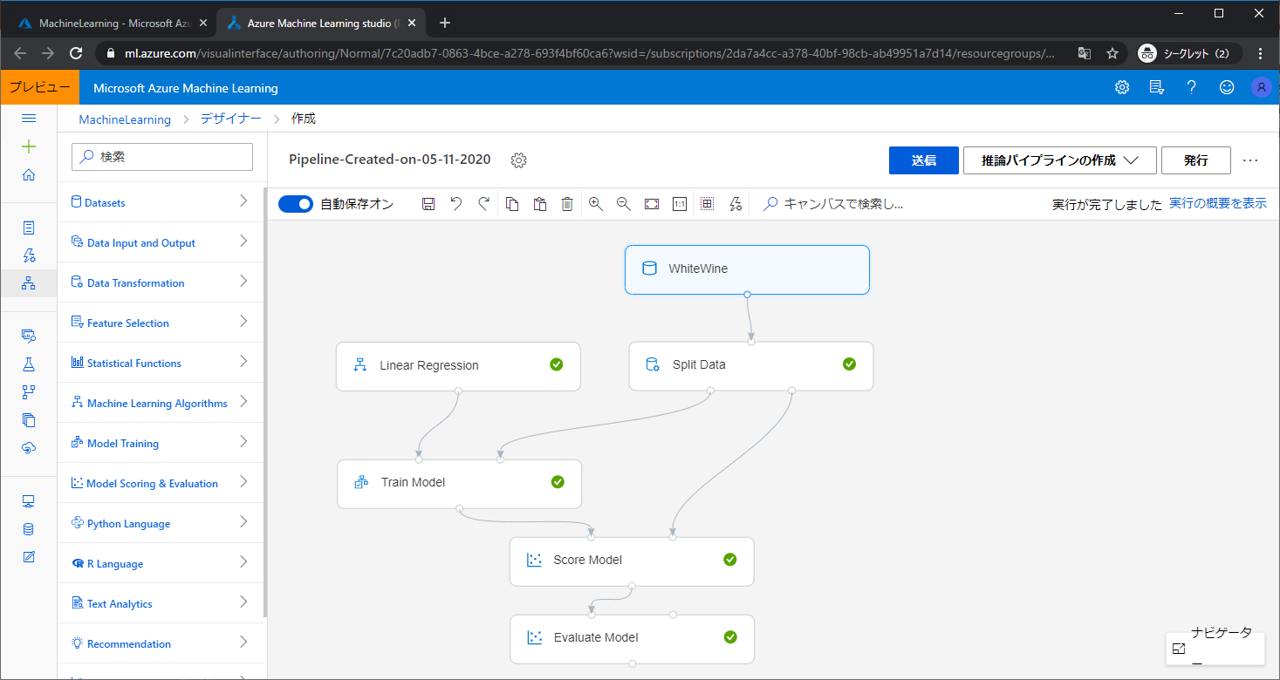
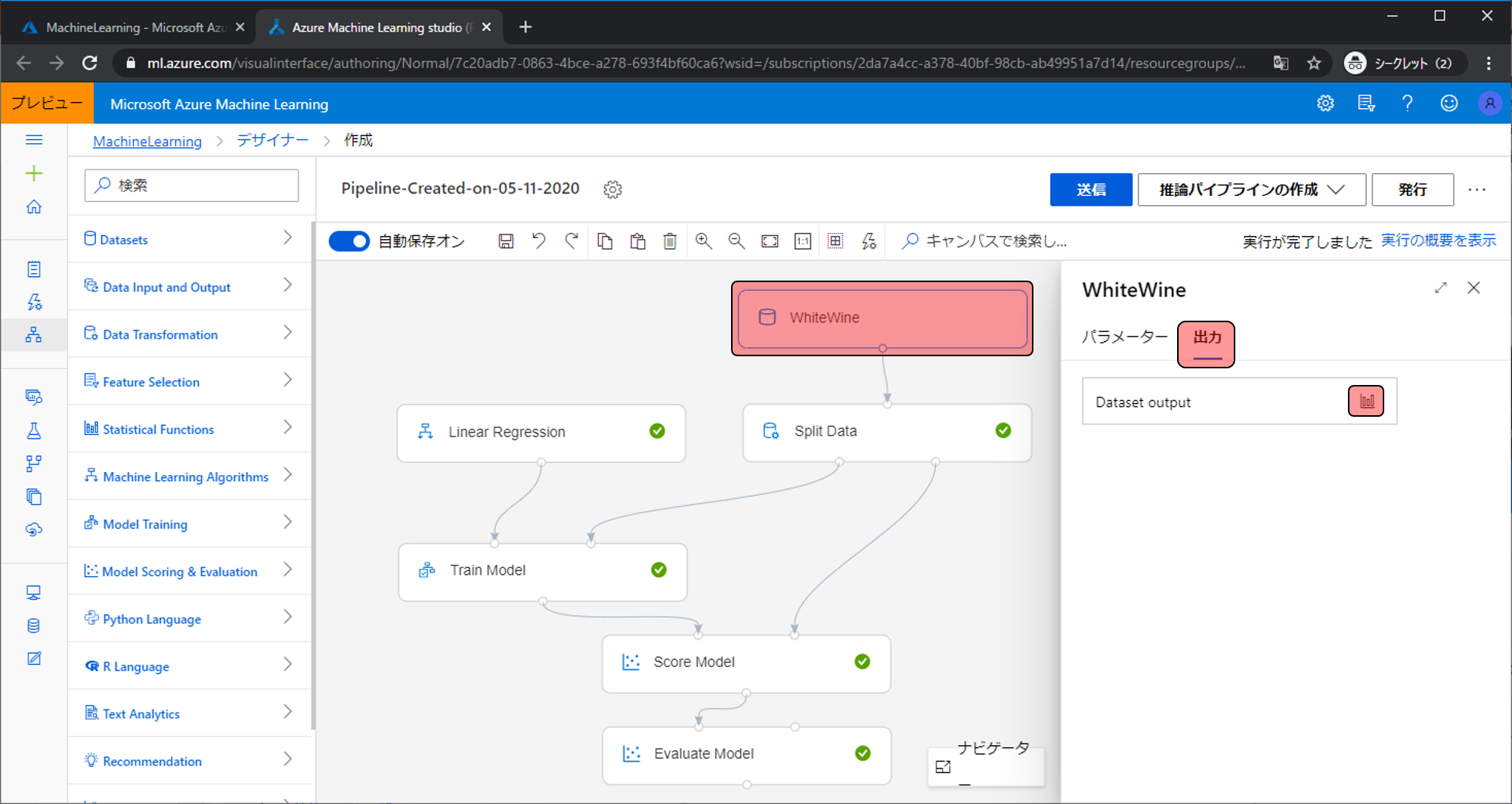
上から見ていきましょう。WhiteWineモジュールは学習させるデータです。どんなデータが出力されているのかを可視化で確認することができます。

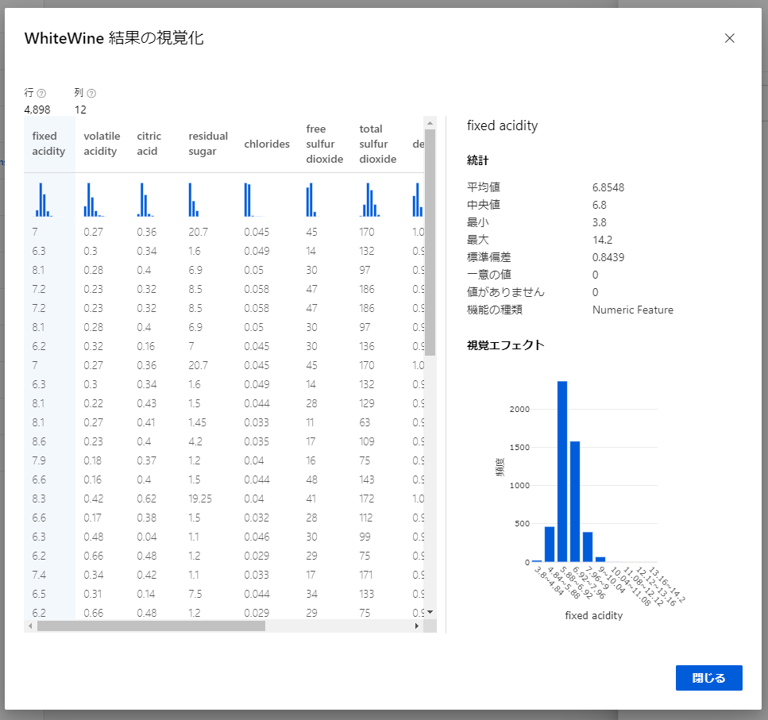
項目をクリックすると、最大値や平均値などの統計情報が確認できます。

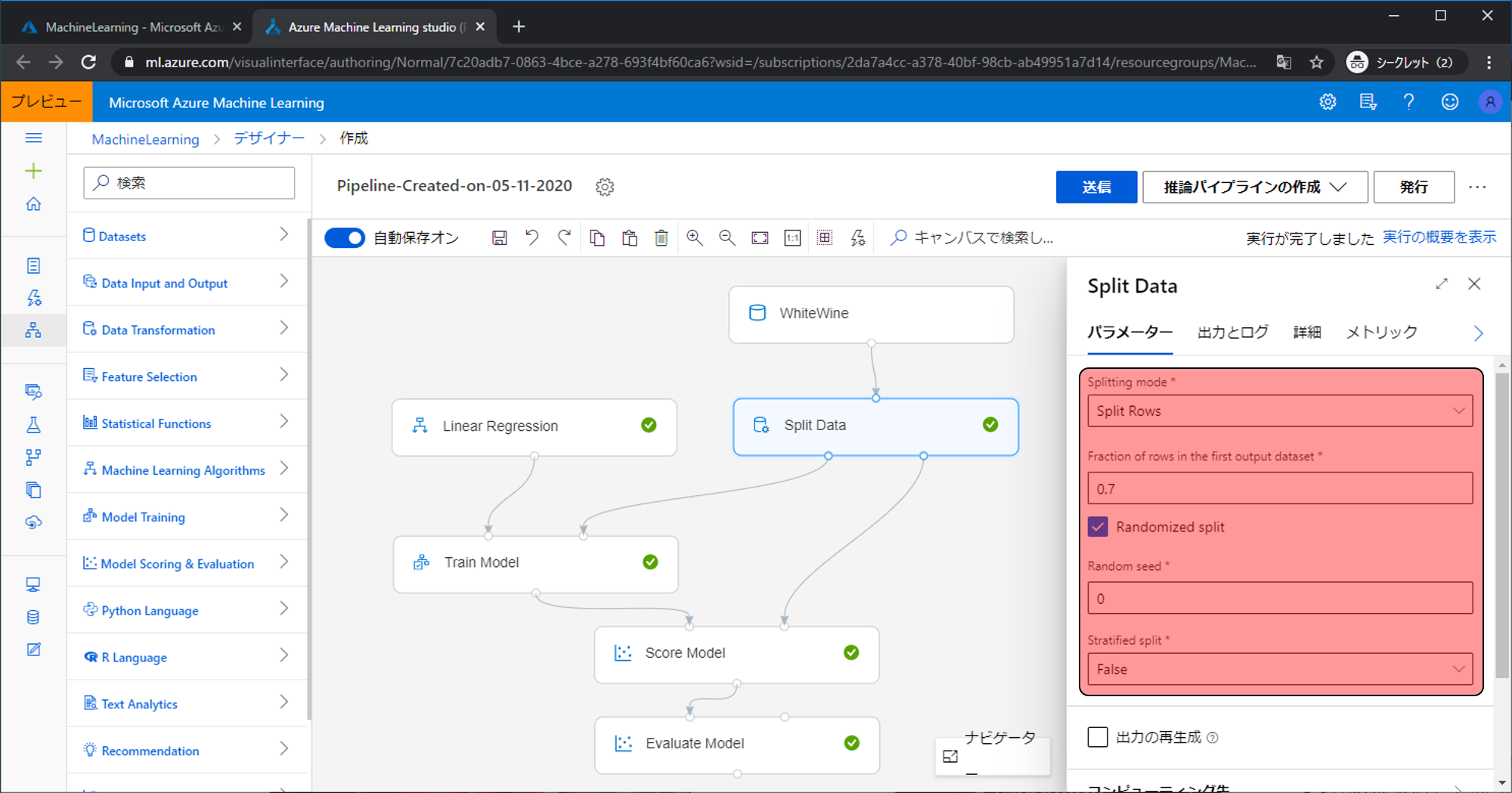
Split Dataの出力も同様に確認することができます。右側の出力がResults dataset1、左側の出力がResults dataset2です。

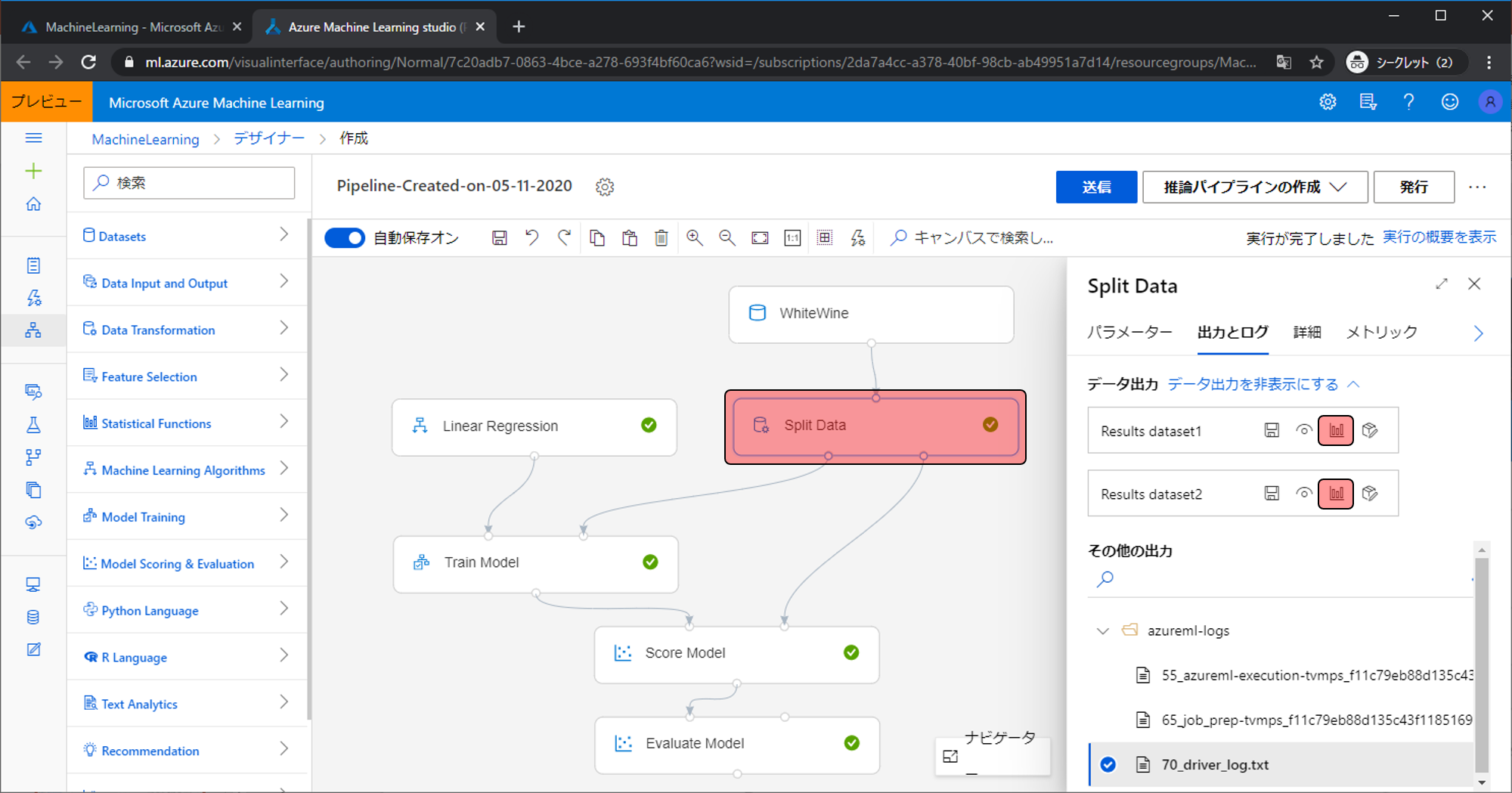
Split Dataのパラメータで設定するパラメータの意味合いは以下になります。

• Splitting mode：Split Rows、Regular Expression Split、Relative Expression Splitの三種類があります。Split Rowsは割合での分割、Regular Expression Splitは正規表現での分割、Relative Expression Splitは数値条件での分割です。今回使ったのはSplit Rowsなので、Split Rowsを選んだ場合のパラメータの解説を行います。
• Fraction of rows in the first output dataset：右と左の出力でデータが出る割合を調整できます。0.5だと100件のデータが入力されていた場合は右から50件、左から50件出力されます。0.7にした場合は、右から70件、左から30件出力されます。
• Randomize Split：チェックを入れずにFraction of rows in the first output datasetにして0.7で分割すると、入力されデータの上から70%を右側の出力、残りの30%を出力します。チェックを入れると上からでなくランダムに分割します。
• Random seed：ランダムのシード値です。数を変えると分割の内容が変わります。シード値なので値の大きさなどに意味は持ちません。
• Stratified split：Trueにすると入力されたデータのカラム（fixed acidityやquality）を指定でき、その内容の割合が同じ様になるように分割します。
  例えば、入力データの100件のうち、Aというデータが80件、Bというデータが20件の場合、分割するとき割合を0.7で完全ランダムに分割すると、右の出力からはAが70件、Bが0件、左の出力からAが10件、Bが20件になり、右側に全くBのデータがない事が起こりえます。それを防ぐためにTrueにすることで右側の出力からAが56件、Bが14件、左側の出力からはAが16件、Bが4件になり、右と左両方の出力でAとBの割合が同じになります。

今回はワインの評価を予測するためにLinear Regression（線形回帰）をしましたが、他にも様々なアルゴリズムが用意されています。アルゴリズムは大きく分類すると3種類あります。Regression、Classification、Clusteringです。

Regressionは身長や体重など数値データを予測したいときに利用します。
Classificationは性別や場所など数値ではないタグのような情報を予測したときに利用します。
Clusteringはなにかの予測をするのではなく、データ群を入力すると似ているデータを分類してくれます。

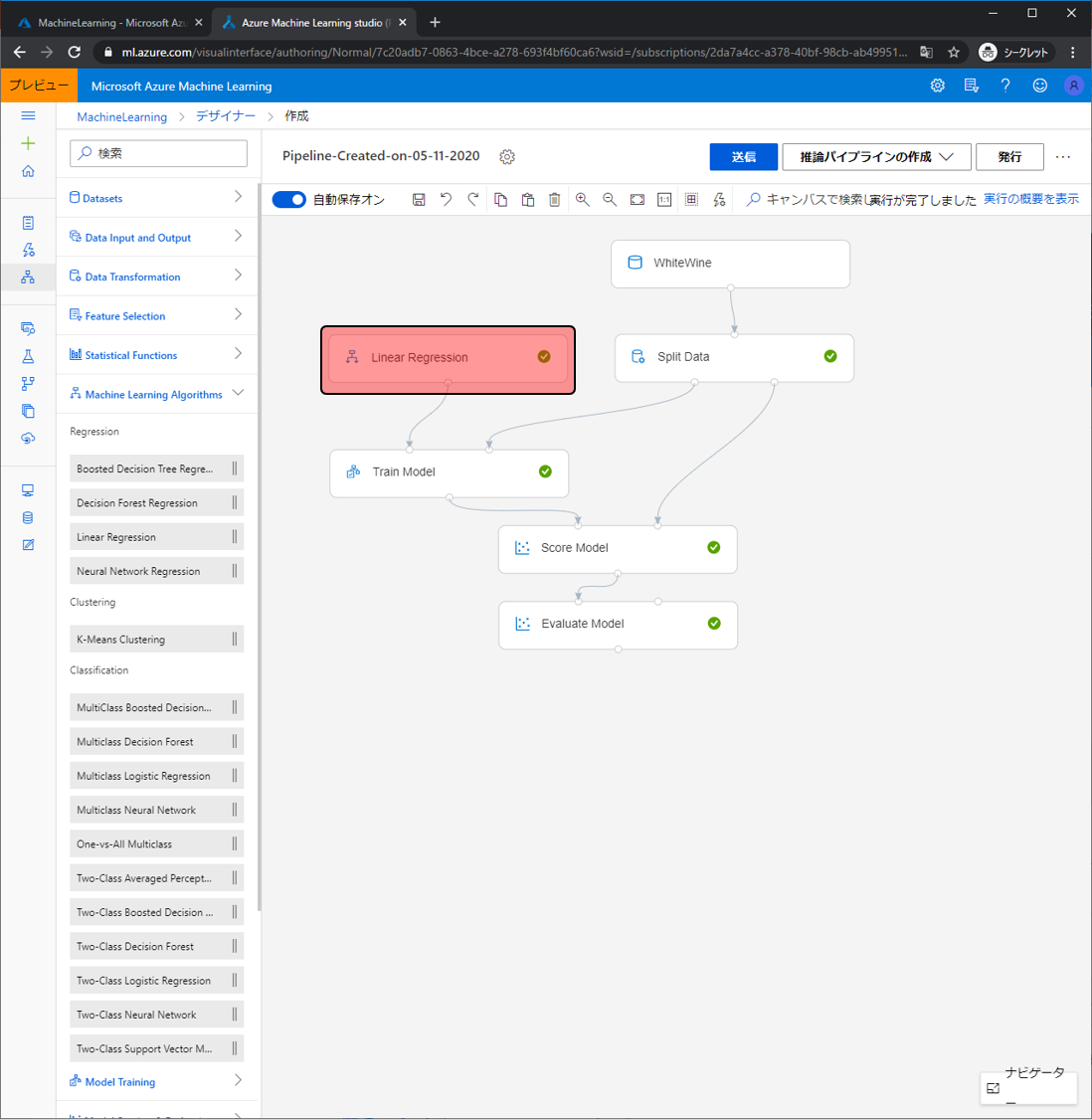
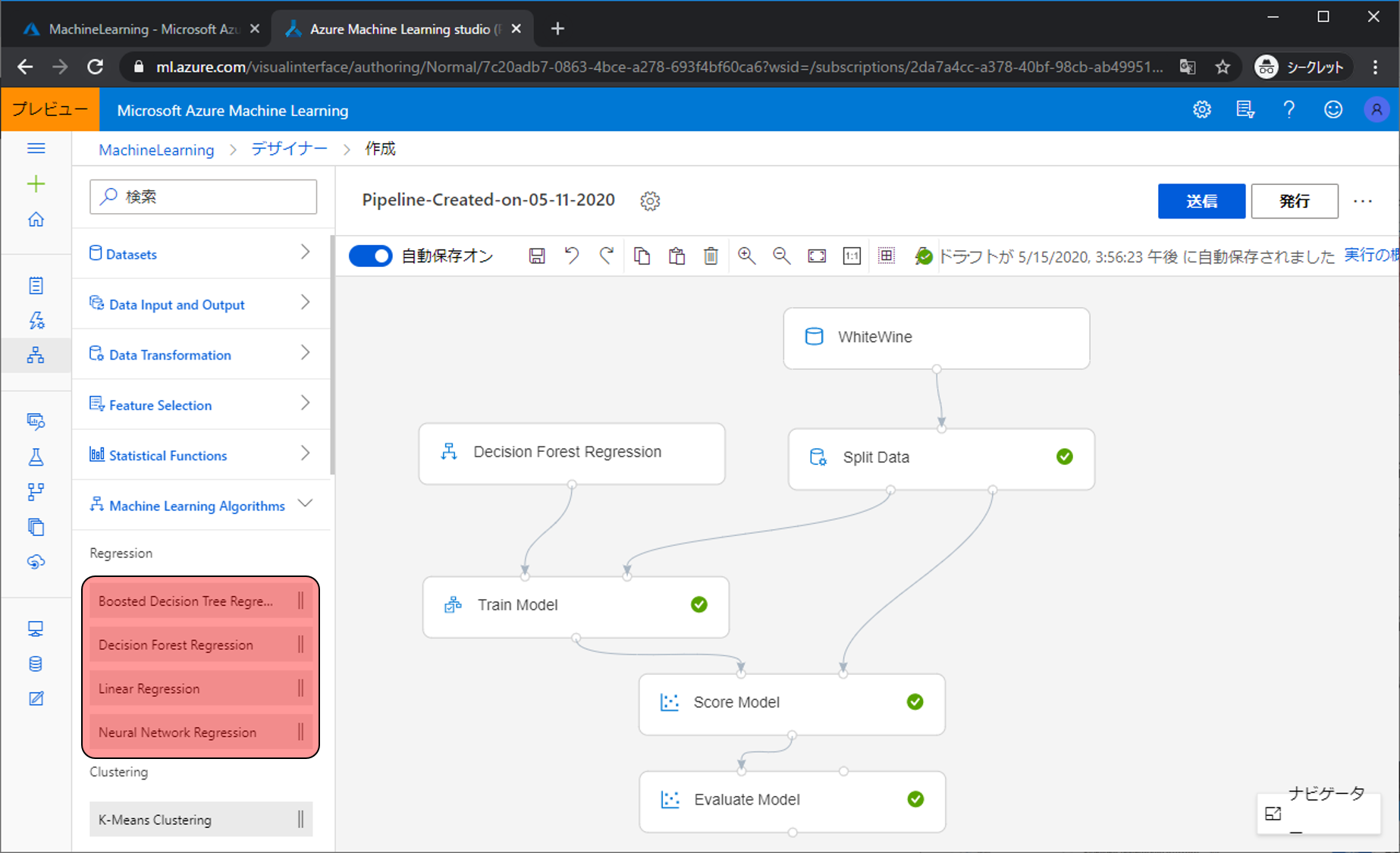
Linear Regressionモジュールを別のRegressionモジュールと置き換えるだけで、違ったアルゴリズムを使ったモデル作成ができます。

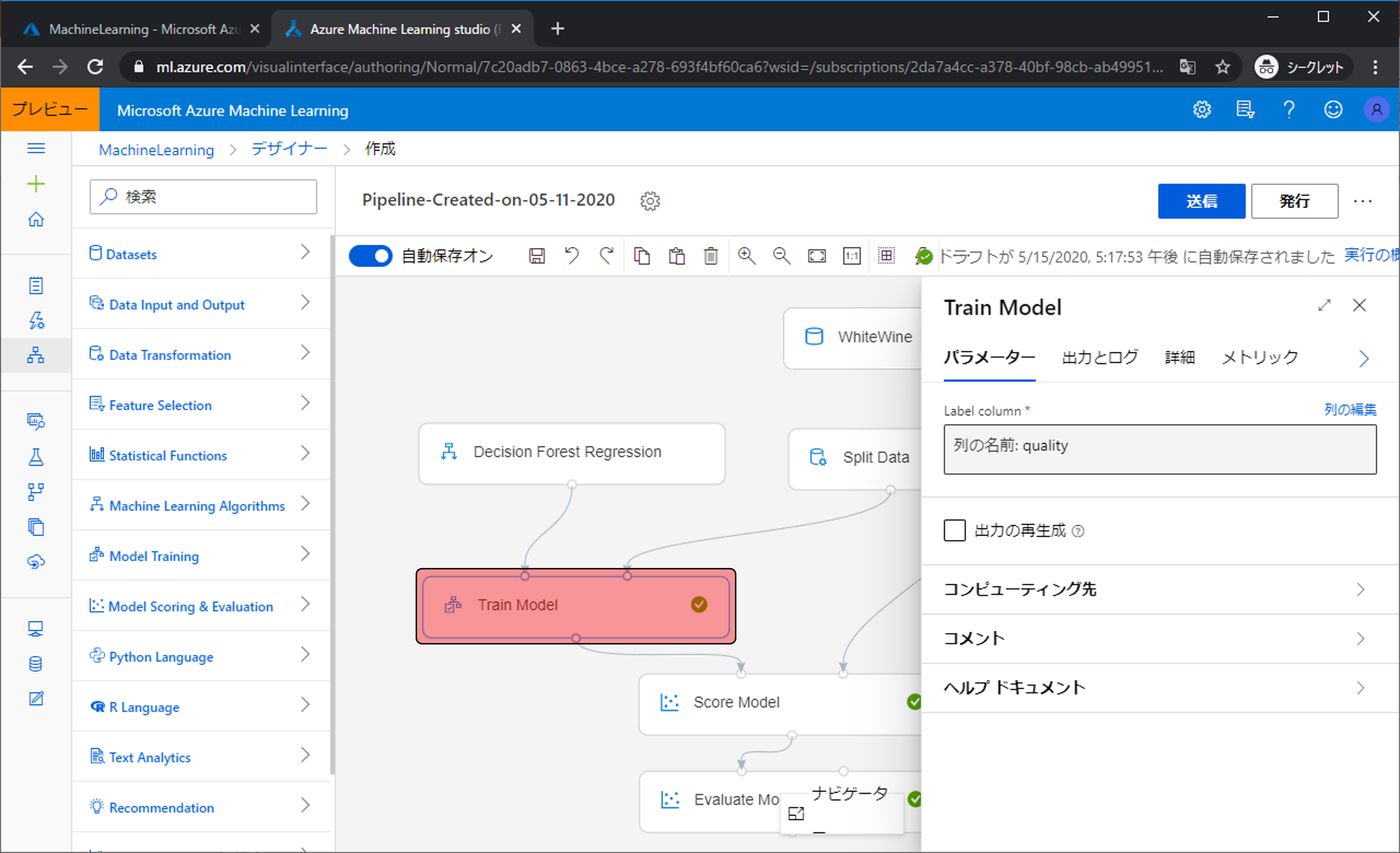
Train Modelでは、パラメータで予測対象を指定しています。この予測対象をquality（品質）からalcohol（アルコール度数）などに変更すると、予測モデルはqualityを含めた他の情報からアルコール度数を予測するようになります。

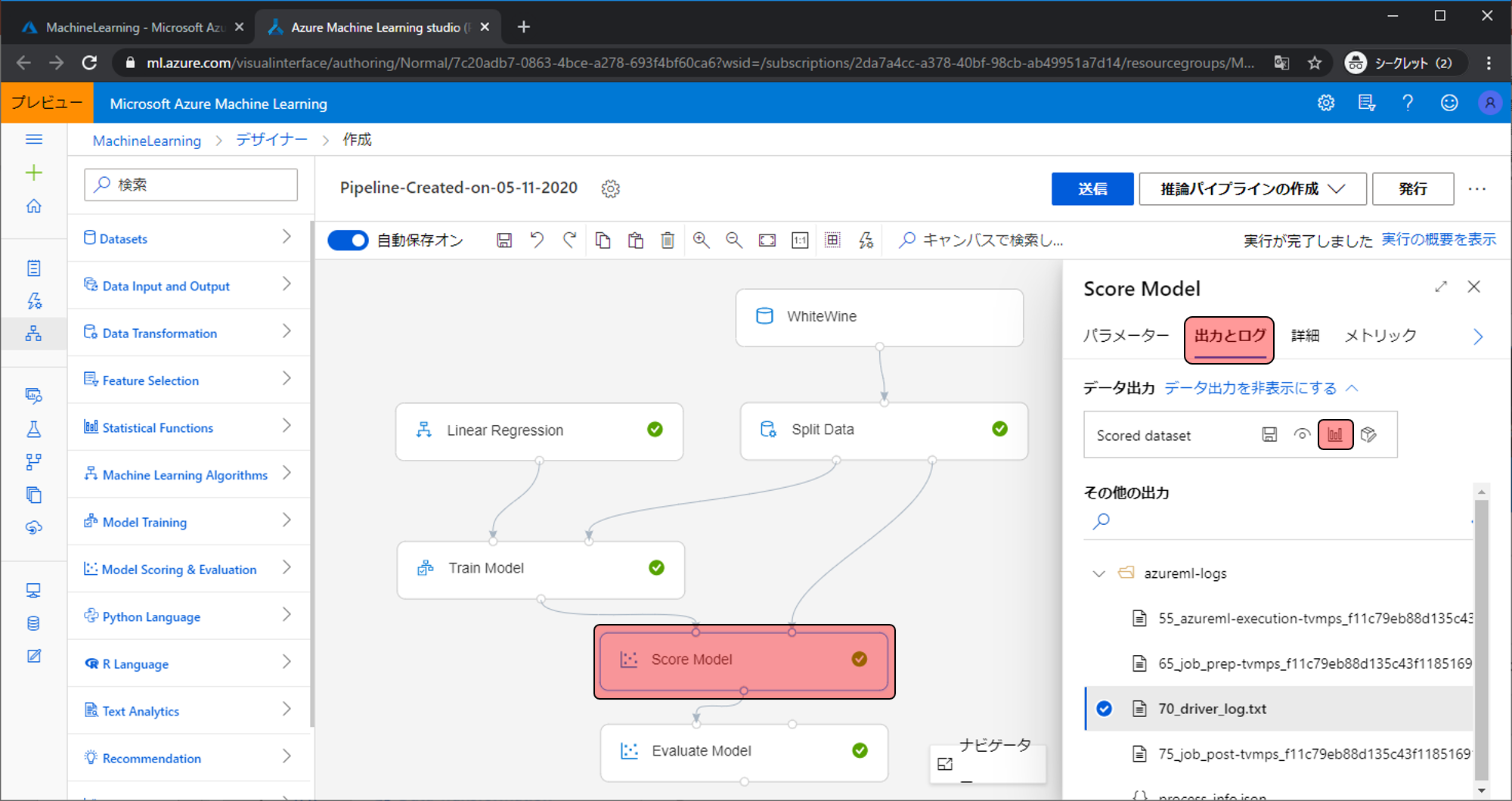
Score Modelで実際にどんな予測をしているのか見てみましょう。Score Modelをクリックし、出力とログの可視化ボタンをクリックします。

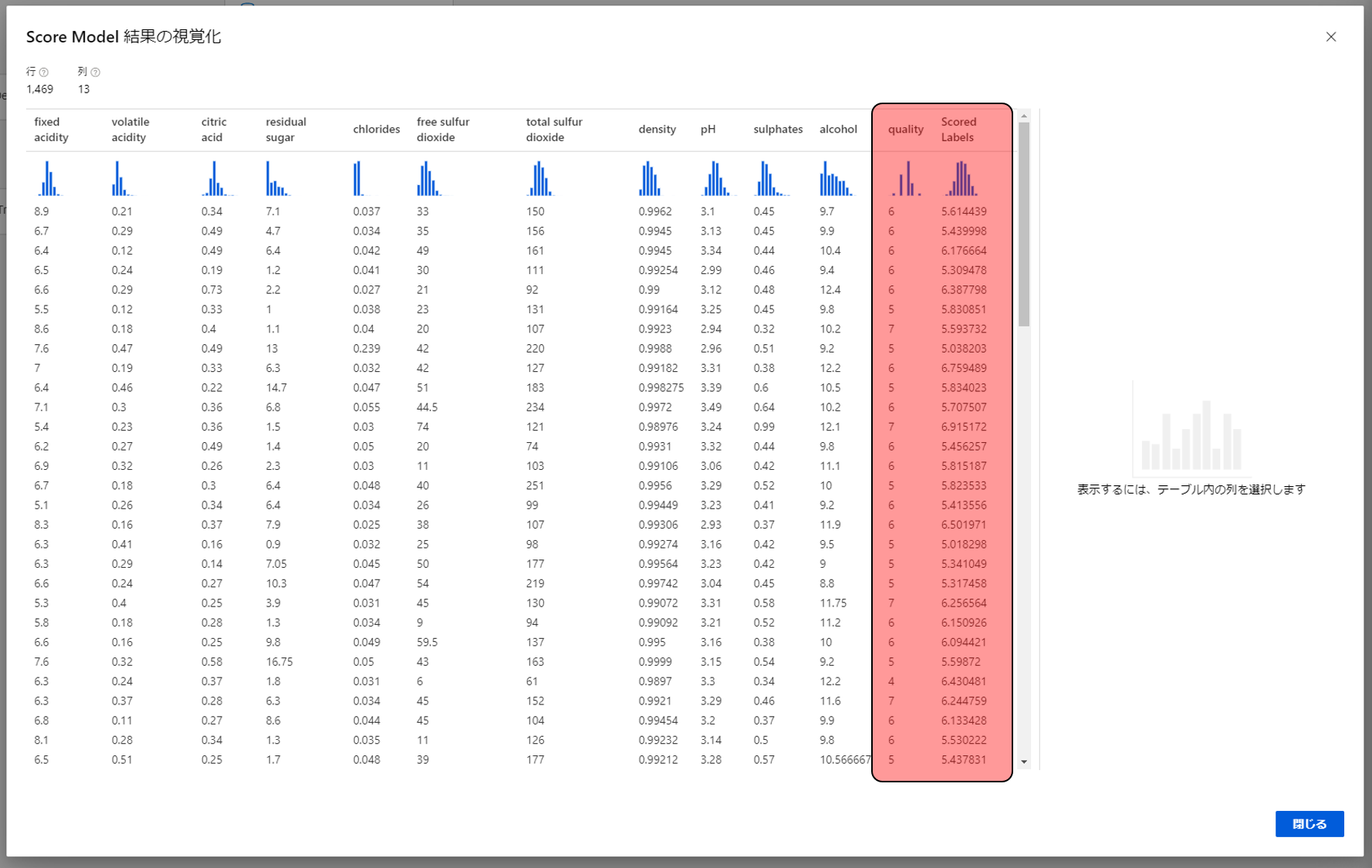
Scored Labelsに予測した値が表示されます。qualityの値と比較するとどのくらい合っているのかがわかります。

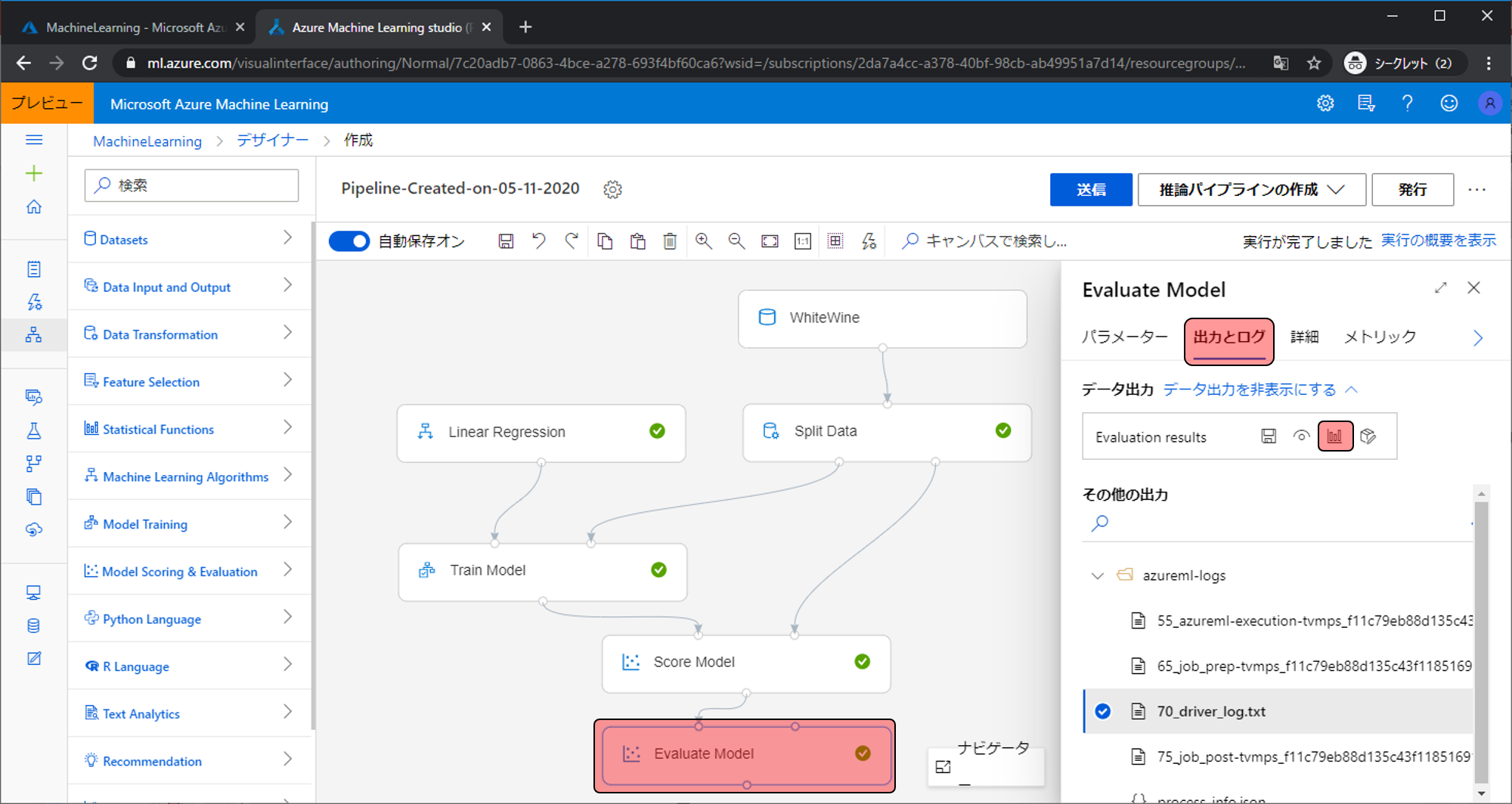
前回解説できなかったモデルの評価確認方法を解説します。Evaluation Modelをクリックして出力とログの視覚化をクリックします。

各項目がモデルの評価を表しています。モデルの評価項目は利用するアルゴリズムによってことなります。今回はLinear Regressionを利用したときの評価項目です。

• Mean_Absolute_Error：平均絶対誤差→0に近いほどよい。予測値と実際の値の大きなズレの影響を受けにくい。
• Root_Mean_Squared_Error：平均平方二乗誤差→0に近いほどよい。測値と実際の値の大きなズレの影響を受けやすい。
• Relative_Squared_Error：相対二乗誤差→0に近いほどよい。
• Relative_Absolute_Error：相対絶対誤差→0に近いほどよい。
• Coefficient_of_Determination：決定係数→1に近いほど良い

これらの項目は計算式から求められますが、その式を理解することはあまり重要ではないのと他の方々が散々解説しているので、ここでは見方だけにとどめておきます。

今回のモデルは決定係数が0.2ととても低いのであまり良くないことが伺えます。また、平均絶対誤差が0.58くらいに対して、平均平方二乗誤差は0.72と２つの差が0.14程度あるので測値と実際の値の大きなズレがそこそこ存在していることが伺えます。

され、ここまでで今回作ったモデルの解釈を行ってきましたが、モデルの評価情報を見るかぎり、あまりいいモデルでないことがわかります。

なので、次回はこのモデルの精度を上げる方法を解説したいと思います。