こんにちは、2023年入社の香月と申します。
今回は私が卒業研究で役立てた知識の1つを紹介しようと思います。
私の研究テーマをざっくり要約すると「現実の池の生態系をPCのシミュレーション上で再現する」というものです。池には当然様々な生物が潜んでおり(あまりにも汚い場合を除く)それぞれの生物に寿命、産卵、エサ、食う食われるの関係...等が成り立っている訳です。
これらの項目をどうやって現実と同じようにPC上に再現するのか。これが一番の課題でもありました。寿命なんで個体同士でバラバラ、産卵時期が来てもどのタイミングで産卵するのかもバラバラ。バラバラなことだらけでした。ランダムを使用して実装しようか悩みましたが、果たしてそれが現実と同じなのか?とも思います。そこで役立ったのが正規分布です。
正規分布とは?
知ってる人も多いと思いますが、一応説明を挟みます。
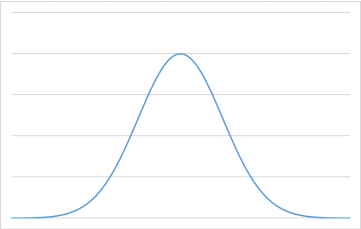
この形の分布を正規分布といいます。多分高校数学とかでやったと思います。(自分は覚えてないです)
自然界の様々な現象はこの分布に従うと言われているらしいです...例えば寿命の分布などは平均寿命である80をピークにして山なりになっており似た形をしていますよね
私はこれをもしかしたら研究にも役立てる?と思い早速実装を試みますが難しそうです。ちょっとランダムな正規分布を作ろうとしますが上手くいかず、そこで見つけたのがゴルトンボードです。
ゴルトンボード

こちらがゴルトンボードです。実物が著作権的都合で貼れず、PowerPointで作成した雑な図であることをご了承ください。パチンコみたいですね。一応おもちゃの分類らしく、amazonで売ってました。
これと正規分布になんの関係が?という話なんですが赤い丸の位置からたくさんボールを落とした際、下の6つの箱にボールはたまりますよね?その形が正規分布っぽくなります。

汚くてごめんなさい。本当なら物理演算等でやるべきなのかもしれませんが、技術不足をお許しください。きれいな分布ではないですが、面白い形をしますよね。
ではこちらをプログラムで再現して研究に役立てるためにちょっと数学っぽくします

赤いボールが青い障害物にぶつかると50/50で左右のどちらかに落ちます。
落ちた位置それぞれに左から番号を振ります。
すると、赤いボールが落ちていく過程で5回50/50ガチャを経過するわけです。
ここで、赤いボールにポイントを追加しましょう。このポイントは50/50ガチャをする時、左に落ちることが決まれば+0ポイント、右に落ちることが決まれば+1ポイントとしましょう。
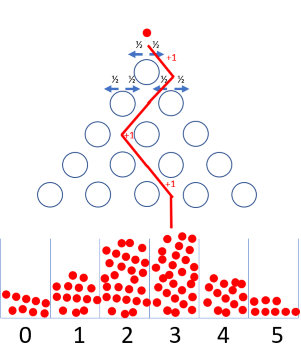
するとボールが落ちていく中でポイントが計算され、そのポイントと下の箱の番号が一致することが分かるかと思います。
プログラムへ実装
数学っぽくまとめれたので、プログラムで再現していきます。使う言語はC++ですが、コメントアウトも追加してがんばってわかりやすく書きます。
C++#include <iostream>
using namespace std;
int stack=5;//障害物の段数、画像だと5
int galton(void){//ゴルトンボード実行関数
int pos=0;//ポイント
for(int i = 0; i < stack; i++){
pos += rand() % 2;//50/50のガチャをして結果の数字[0,1]を足します。
}
return pos;
}
int main(void){
int balls;
cin >> balls;//ボールの数を入力
int ans[balls];//各ボールがどの箱に落ちたかを記録
int result[stack+1];//どの箱にいくつボールが入ったのか記録する配列、要素数は段数+1
for(int i = 0; i < stack+1; i++){//resultの初期化
result[i] = 0;
}
for(int i = 0; i < balls; i++){
ans[i] = galton();//関数を実行して結果を保存
}
for(int i = 0; i < stack+1; i++){
for(int j = 0; j < balls; j++){
if(ans[j] == i){//箱に入っているボールを数える
result[i] ++;
}
}
}
for(int i = 0; i < stack+1; i++){
cout << result[i] << " ";//表示
}
}
雑なコードをお許しください。修正箇所たくさんあると思います。
ボールの数を1000としたとき、実行結果はこのようになりました。
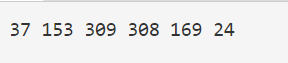
グラフに落とし込むとこんな感じです。
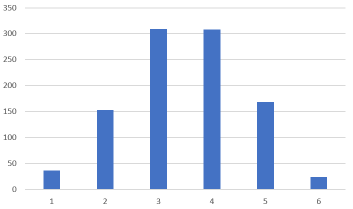
正規分布っぽくなりました。
おもちゃからの応用で楽に正規分布を再現できました。
この情報がなにかの役に立つことを願います。
長々と書いてしまいましたが以上になります。ありがとうございました。なんだかレポート書いてる気分になりました。







![Microsoft Power BI [実践] 入門 ―― BI初心者でもすぐできる! リアルタイム分析・可視化の手引きとリファレンス](/assets/img/banner-power-bi.c9bd875.png)
![Microsoft Power Apps ローコード開発[実践]入門――ノンプログラマーにやさしいアプリ開発の手引きとリファレンス](/assets/img/banner-powerplatform-2.213ebee.png)
![Microsoft PowerPlatformローコード開発[活用]入門 ――現場で使える業務アプリのレシピ集](/assets/img/banner-powerplatform-1.a01c0c2.png)


